Lösung von Zusatzaufgabe 11.2P (SoSe 13): Unterschied zwischen den Versionen
| Zeile 29: | Zeile 29: | ||
<br /> | <br /> | ||
Jetzt weiss ich net wie ich es schreiben soll dass der Abstand doppelt so groß ist. Ich weis das die Verkettung zweier Geradenspiegelungen an parallelen Geraden durch eine Verschiebung ersetzt werden können. Aber wie soll ich es anwenden. ?? Kann mir jemand helfen??;-///--[[Benutzer:Blumenkind|Blumenkind]] 23:52, 12. Jul. 2013 (CEST)Blumenkind 23:50, 13.Juli | Jetzt weiss ich net wie ich es schreiben soll dass der Abstand doppelt so groß ist. Ich weis das die Verkettung zweier Geradenspiegelungen an parallelen Geraden durch eine Verschiebung ersetzt werden können. Aber wie soll ich es anwenden. ?? Kann mir jemand helfen??;-///--[[Benutzer:Blumenkind|Blumenkind]] 23:52, 12. Jul. 2013 (CEST)Blumenkind 23:50, 13.Juli | ||
| + | |||
| + | |||
Sorry, habe währenddessen eine eigene Version erarbeitet.<br /> | Sorry, habe währenddessen eine eigene Version erarbeitet.<br /> | ||
Version vom 12. Juli 2013, 23:00 Uhr
Beweisen Sie Satz IX.9:
Gegeben seien zwei zueinander parallele Spiegelgeraden a und b. Wir betrachten die Verkettung 
. Jeder Punkt P hat dabei zu seinem Bildpunkt 
einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.
Hinweis: Hier genügt ein exemplarischer Beweis für eine mögliche Lage von P. Nehmen wir doch mal an, P und seine Spiegelpunkte liegen so:
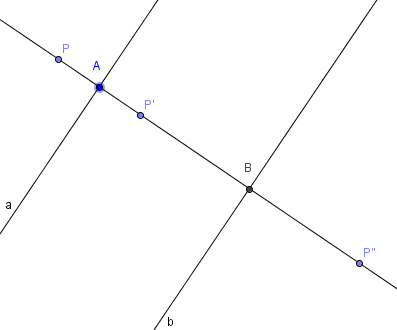
--Tutorin Anne 17:30, 12. Jul. 2013 (CEST)
| Voraussetzung | aIIb, Sa o Sb (P) = P``, g senkrecht zu a, g senkrecht zu b sowie g geschnitten a= (A) und g geschnitten b = B, |
| Behauptung | Abstand ist doppelt groß von P zu P`` |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | Sa(P)=P´und Sb(P`)=P``mit P, P`und P``Element g | Def. Sg., Vor. |
| 2 | IStrecke PAI= IAP`I und IP`BI=IStreckeBP`Ì sowie PP`senkrecht a und P`P``senkrecht g | (1), Voraussetzung, Konstruktion |
| 3 | P``ist eine Verschiebung in Richtung PP``und PP``ist Richtungsgleich zu AB | (2), Vor. |
| 4 | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
Jetzt weiss ich net wie ich es schreiben soll dass der Abstand doppelt so groß ist. Ich weis das die Verkettung zweier Geradenspiegelungen an parallelen Geraden durch eine Verschiebung ersetzt werden können. Aber wie soll ich es anwenden. ?? Kann mir jemand helfen??;-///--Blumenkind 23:52, 12. Jul. 2013 (CEST)Blumenkind 23:50, 13.Juli
Sorry, habe währenddessen eine eigene Version erarbeitet.
Ist eine solche ausführliche Voraussetzung erlaubt?
Der Beweis ist sehr lang geworden.
--Nolessonlearned 00:00, 13. Jul. 2013 (CEST)
Voraussetzung:
Sa∘Sb(P) = P(zweistrich) mit a || b
mit koll(P,P',P(zweistrich)
mit P,P',P(zweistrich) ∈ g
mit g ⊥ a ∧ g ⊥ b
mit g ∩ a = {M} ∧ g ∩ b = {N} --Nolessonlearned 18:17, 12. Jul. 2013 (CEST)
Behauptung:
|P͞P(zweistrich)| = 2|ab| ≌ 2(|MP'| + |P'N|) --Nolessonlearned 18:17, 12. Jul. 2013 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | koll(P,P',P(zweistrich) | Eigenschaft GS; Voraussetzung |
| 2) | P' = Sa(P) | Def. GS; Voraussetzung |
| 3) | P(zweistrich) = Sb(P') | Def. GS; Voraussetzung |
| 4) | P͞M͞| ≌ |M͞P͞'| | (1); (2); Voraussetzung; Streckentreue d. GS bzw. Abstandserhaltung |
| 5) | P͞'N͞| ≌ |N͞P͞|(zweistrich) | (1); (2); (3); Voraussetzung; Streckentreue d. GS bzw. Abstandserhaltung |
| 6) | M͞P͞'| + |P͞'N͞| = |ab| | (4); (5); Streckenaddition bzw. Abstandsaddition; Rechnen in ℝ |
| 7) | P͞M͞| ≌ |N͞P͞|(zweistrich) ≌ |M͞P͞'| + |P͞'N͞| | (4); (5); (6); Streckenaddition bzw. Abstandsaddition; Rechnen in ℝ; Eigenschaft der Translation |
| 8) | M͞P͞'| + |P͞'N͞|) ≌ |P͞P͞|(zweistrich) | (6); (7); Streckenaddition bzw. Abstandsaddition; Rechnen in ℝ; Eigenschaft der Translation |
| 9) | P͞P͞|(zweistrich) ≌ 2|ab| | (6); (7); (8) q.e.d |
