Lösung von Aufgabe 10.2: Unterschied zwischen den Versionen
TimoRR (Diskussion | Beiträge) |
|||
| Zeile 28: | Zeile 28: | ||
Da es nach dem Winkelkonstruktionsaxiom genau eine Gerade gibt, die die Eindeutigkeit bereits gezeigt.<br /> | Da es nach dem Winkelkonstruktionsaxiom genau eine Gerade gibt, die die Eindeutigkeit bereits gezeigt.<br /> | ||
qed --[[Benutzer:Löwenzahn|Löwenzahn]] 17:14, 1. Jul. 2010 (UTC) | qed --[[Benutzer:Löwenzahn|Löwenzahn]] 17:14, 1. Jul. 2010 (UTC) | ||
| + | |||
| + | |||
| + | == [[Zweiter Beweisversuch]] == | ||
| + | |||
| + | |||
| + | Voraussetzung: g Element E, s Element E, P Element g | ||
| + | Behauptung: s Element g und s senkrecht auf g | ||
| + | |||
| + | Existenz: | ||
| + | {| class="wikitable center" | ||
| + | |+ Es gibt eine Gerade s Element, die durch den Punkt P geht und senkrecht auf g steht | ||
| + | |- style="background: #DDFFDD;" | ||
| + | ! | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(I) | ||
| + | | Es existiert ein X Element E mit der Eigenschaft, dass X Element S und X Element PX+ | ||
| + | | Axiom I.2 (Gerade hat mindestens 2 Punkte) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(II) | ||
| + | || Es existieren auf der Geraden g ein Punkt P1 auf PP1+ und ein Punkt P2 auf PP1- <br /> |Winkel(XPP2)| = |Winkel(XPP1)| = |w| mit w = 90 | ||
| + | | Definition V.6 (Rechter Winkel) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(III) | ||
| + | | s steht senkrecht auf g | ||
| + | | (II), Definition V.8 (Relation senkrecht) | ||
| + | |} | ||
| + | |||
| + | Eindeutigkeit: | ||
| + | Nach Winkelkonstruktionsaxiom IV.2 gibt es in jeder Halbebene genau nur einen Strahl mit|w|=|Winkel(XPP2)| bzw. |w| = |Winkel(XPP1)| | ||
| + | Nach Winkelmaßaxiom IV.1 gibt es für w genau eine reelle Zahl zwischen 0 und 180. | ||
| + | Nach der Definition V.6, Satz V.3 und Satz V.4 gibt es rechte Winkel mit der Größe 90. | ||
| + | Nach Definition V.8 ist eine Gerade dann senkrecht auf der anderen, wenn bei dem Schnitt der beiden rechte Winkel enstehen. | ||
| + | Somit kann es nur einen Strahl geben in jeder Halbebene, der Senkrecht auf g steht und durch den Punkt P geht. | ||
Version vom 2. Juli 2010, 00:13 Uhr
Beweis Versuch 1:
VSS: 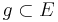 ,
, 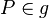
Beh: es gibt genau eine Gerade s durch P, die senkrecht auf g steht
EXISTENZ
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | in  gibt es einen Strahl mit gibt es einen Strahl mit 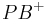
|
Axiom I.2 und Def. Halbgerade |
| (II) | es existiert genau ein Strahl 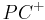 in der Halbebene in der Halbebene 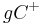 mit mit 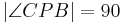
|
Winkelkonstruktionsaxiom, (I) |
| (III) | es exisitiert genau eine Gerade s durch  und und  , senkrecht auf , senkrecht auf 
|
Axiom I.1, (II) |
EINDEUTIGKEIT
Da es nach dem Winkelkonstruktionsaxiom genau eine Gerade gibt, die die Eindeutigkeit bereits gezeigt.
qed --Löwenzahn 17:14, 1. Jul. 2010 (UTC)
Zweiter Beweisversuch
Voraussetzung: g Element E, s Element E, P Element g Behauptung: s Element g und s senkrecht auf g
Existenz:
| Beweisschritt | Begründung | |
|---|---|---|
| (I) | Es existiert ein X Element E mit der Eigenschaft, dass X Element S und X Element PX+ | Axiom I.2 (Gerade hat mindestens 2 Punkte) |
| (II) | Es existieren auf der Geraden g ein Punkt P1 auf PP1+ und ein Punkt P2 auf PP1- |Winkel(XPP2)| = |Winkel(XPP1)| = |w| mit w = 90 |
Definition V.6 (Rechter Winkel) |
| (III) | s steht senkrecht auf g | (II), Definition V.8 (Relation senkrecht) |
Eindeutigkeit: Nach Winkelkonstruktionsaxiom IV.2 gibt es in jeder Halbebene genau nur einen Strahl mit|w|=|Winkel(XPP2)| bzw. |w| = |Winkel(XPP1)| Nach Winkelmaßaxiom IV.1 gibt es für w genau eine reelle Zahl zwischen 0 und 180. Nach der Definition V.6, Satz V.3 und Satz V.4 gibt es rechte Winkel mit der Größe 90. Nach Definition V.8 ist eine Gerade dann senkrecht auf der anderen, wenn bei dem Schnitt der beiden rechte Winkel enstehen. Somit kann es nur einen Strahl geben in jeder Halbebene, der Senkrecht auf g steht und durch den Punkt P geht.

