Der Inkreis und die Winkelhalbierenden eines Dreiecks: Unterschied zwischen den Versionen
(→Definition Winkelhalbierende:) |
(→Winkelhalbierendekriterium) |
||
| Zeile 14: | Zeile 14: | ||
<br /><br /> | <br /><br /> | ||
| − | Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 07:01, 19. Jul. 2010 (UTC): Was zu beweisen wäre. | + | Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 07:01, 19. Jul. 2010 (UTC): Was zu beweisen wäre.<br /> |
| + | |||
| + | |||
| + | <u>Entspricht das nicht der Aufgabe im Tutorium 13 Nr.1???:</u> | ||
| + | Gegeben sei ein (nicht gestreckter) Winkel <math> \angle AOB</math>, es sei <math> \overline {OA} \cong \overline {OB} </math> und <math> P \in \overline {AB} </math>.<br /> | ||
| + | Dann ist <math> OP^+ </math> genau dann Winkelhalbierende von <math> \angle AOB </math>, wenn <math> P </math> Mittelpnkt von <math> \overline {AB} </math>.--[[Benutzer:Löwenzahn|Löwenzahn]] 17:42, 19. Jul. 2010 (UTC) | ||
=== Satz über die Winkelhalbierenden eines Dreiecks === | === Satz über die Winkelhalbierenden eines Dreiecks === | ||
Version vom 19. Juli 2010, 19:42 Uhr
Inhaltsverzeichnis[Verbergen] |
Definition Winkelhalbierende:
Ein Winkelhalbierende eines Winkels <ASB ist ein Strahl SP+, der im Inneren des Winkels <ASB liegt und den Winkel <ASB halbiert.
Kommentar --*m.g.* 06:49, 19. Jul. 2010 (UTC): Der Begriff Winkelhalbierende wurde bereits definiert: Definition_VI.2. Analog zum Begriff der Mittelsenkrechten eines Dreiecks (Die Definition war am Freitag noch nicht im Skript.) müsste es hier darum gehen, zu definieren, was unter den Winkelhalbierenden eines Dreiecks zu verstehen ist. (Ist trivial, wäre aber formal nötig.)
Definition Winkelhalbierende eines Dreiecks:
Unter den Winkelhalbierenden eines Dreiecks versteht man die Winkelhalbierende der Innenwinkel des Dreiecks.--Löwenzahn 17:36, 19. Jul. 2010 (UTC)
Winkelhalbierendekriterium
Eine Punktmenge ist genau dann Winkelhalbierende eines Winkels <ASB, wenn sie alle Punkte enthält, die im Inneren des Winkels liegen und die zu den Schenkeln SA+ und SB+ den gleichen Abstand haben.
Kommentar --*m.g.* 07:01, 19. Jul. 2010 (UTC): Was zu beweisen wäre.
Entspricht das nicht der Aufgabe im Tutorium 13 Nr.1???:
Gegeben sei ein (nicht gestreckter) Winkel 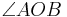 , es sei
, es sei 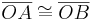 und
und 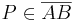 .
.
Dann ist 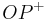 genau dann Winkelhalbierende von
genau dann Winkelhalbierende von 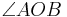 , wenn
, wenn  Mittelpnkt von
Mittelpnkt von  .--Löwenzahn 17:42, 19. Jul. 2010 (UTC)
.--Löwenzahn 17:42, 19. Jul. 2010 (UTC)
Satz über die Winkelhalbierenden eines Dreiecks
Die Winkelhalbierenden eines Dreiecks schneiden sich genau in einem Punkt. Dieser Punkt heißt Inkreismittelpunkt.
Alternativ: Jedes Dreieck besitzt genau einen Inkreis.
--Tja??? 12:53, 18. Jul. 2010 (UTC)
Kommentar --*m.g.* 06:45, 19. Jul. 2010 (UTC): Was unter dem Inkreis eines Dreiecks zu verstehen ist, wird definiert. Jeder Kreis hat genau einen Mittelpunkt. Könnte man jetzt nicht beweisen, dass der Schnittpunkt der Winkelhalbierenden der Inkreismittelpunkt ist? Einfach nur noch mal über die Wortwahl "heißt" nachdenken.
Inkreis eines Dreiecks
Definition Inkreis
Ein Kreis, der alle drei Seiten eines Dreiecks in jeweils genau einem Punkt berührt, heißt Inkreis des Dreiecks.--Löwenzahn 15:25, 18. Jul. 2010 (UTC)
Hab ein schönes Bild hierzu gemalt :) http://wikis.zum.de/geowiki/index.php/Bild:IMAG0040.JPG --Principella 22:07, 18. Jul. 2010 (UTC)
Ist "berühren" nicht was anderes als "schneiden"?--Vankman 16:55, 19. Jul. 2010 (UTC) Wie ist denn die Definition von "berühren"? Die Berührung zweier mathematischer Kurven ist, in einem gemeinsamen Punkt (Berührpunkt) übereinstimmende Tangenten zu haben....(aus wiki) Wäre dann die Definition nicht doch korrekt?--Vankman 16:58, 19. Jul. 2010 (UTC)

