Lösung Aufgaben 11 (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 11.5)
(→‎Aufgabe 11.6)
Zeile 48: Zeile 48:
  
 
[[Lösung von Aufg. 11.6 (SoSe_11)]]
 
[[Lösung von Aufg. 11.6 (SoSe_11)]]
−
Es seien α und β zwei Nebenwinkel mit| α|=|β|.  Nach dem Axiom 4|4 sind α und βsupplementär, was | α|=|β| =180 bedeutet. Die Winkel α und β sind rechte Winkel und haben damit dieselbe Größe. Damit gilt | α|=|β| =180/2 = 90.
+
 
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]

Version vom 30. Juni 2011, 13:29 Uhr

Inhaltsverzeichnis

Aufgabe 11.1

Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen?

a) 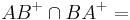\ AB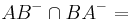^{+} \c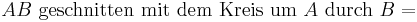ap BA^{+} =

b) \ AB^{-} \cap BA^{-} =

c) \ AB \mathrm{~geschnitten~mit~d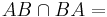em~Kreis~um} \ A \mathrm{~durch} \ B =

d)\ AB \cap BA =

Lösung von Aufg. 11.1 (SoSe_11)


Aufgabe 11.2

Definieren Sie den Begriff Strahl \ AB^{+}. Verwenden Sie dabei den Begriff Strecke.

Lösung von Aufg. 11.2 (SoSe_11)


Aufgabe 11.3

Definition (gemeiner Dreiecksschneider): Unter einem gemeinen Dreieckschneider versteht man eine Gerade, die alle drei offenen Seiten eines Dreiecks schneidet.

Beschreiben Sie die Menge aller gemeinen Dreiecksschneider und begründen Sie Ihre Aussage.

Lösung von Aufg. 11.3 (SoSe_11)


Aufgabe 11.4

Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:

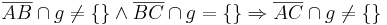
\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace \Rightarrow \overline{AC} \cap g \neq \lbrace \rbrace

Lösung von Aufg. 11.4 (SoSe_11)

Aufgabe 11.5

Beweisen Sie: Jeder rechte Winkel hat das Maß 90.

Lösung von Aufg. 11.5 (SoSe_11) 

Es seien α und β zwei Nebenwinkel mit| α|=|β|. Nach dem Axiom 4|4 sind α und βsupplementär, was | α|=|β| =180 bedeutet. Die Winkel α und β sind rechte Winkel und haben damit dieselbe Größe. Damit gilt | α|=|β| =180/2 = 90.

Aufgabe 11.6

Definition V.9 : (noch mehr Senkrecht)

Eine Gerade \ g und eine Strecke \overline{AB} stehen senkrecht aufeinander, wenn \ g und die Gerade \ AB senkrecht aufeinander stehen.

Ergänzen Sie:

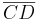Eine Strecke \ \overline{AB} und eine Strecke \ \overline{CD} stehen senkrecht aufeinander, wenn ... .
Eine Gerade \ g und eine Ebene \epsilon stehen senkrecht aueinander, wenn es in \epsilon ... .

Lösung von Aufg. 11.6 (SoSe_11)

Von „http://geometrie.zum.de/index.php?title=Lösung_Aufgaben_11_(SoSe_11)&oldid=7927“