Lösung von Aufgabe 2.7 (WS 11/12): Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
| + | |||
| + | Wenn eine Halbgerade SP+ den Scheitelpunkt S eines Winkels <math>\angle ASB</math> schneidet und es gilt <math>\angle ASP</math> = <math>\angle PSB</math>, dann ist SP+ eine Winkelhalbierende.--[[Benutzer:Lindi 88|Lindi 88]] 19:43, 24. Okt. 2011 (CEST) | ||
Version vom 24. Oktober 2011, 18:43 Uhr
Geben Sie eine exakte Definition des Begriffs Winkelhalbierende an (orientieren Sie sich gegebenenfalls an Schulbuchdefinitionen). Notieren Sie, welche anderen Begriffe Sie dazu verwenden.
Die Winkelhalbierende, ist die Gerade, welche bei einer geometrischen Figur einen Eckpunkt so schneidet, dass der Winkel der beiden Strecken welche diesen Eckpunkt dieser Figur bilden, in zwei gleich große Winkel geteilt wird. --RicRic
- Ist die Winkelhalbierende eine Gerade oder, wie unten beschrieben, eine Halbgerade? Und sind die Schenkel eines Winkels Strecken, Geraden oder Halbgeraden? Es ist wichtig, dass man hier die richtigen Bezeichnungen verwendet und klar unterscheidet.--Tutor Andreas 17:47, 23. Okt. 2011 (CEST)
Eine Winkelhalbierende ist eine Halbgerade, die durch den Scheitelpunkt eines Winkels verläuft und das Winkelfeld in zwei kongruente Teile teilt. --CaroDa 12:36, 23. Okt. 2011 (CEST)
- Was ist ein Winkelfeld? --Tutor Andreas 17:47, 23. Okt. 2011 (CEST)
Wenn eine Halbgerade SP+ den Scheitelpunkt S eines Winkels  schneidet und es gilt
schneidet und es gilt 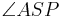 =
= 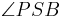 , dann ist SP+ eine Winkelhalbierende.--Lindi 88 19:43, 24. Okt. 2011 (CEST)
, dann ist SP+ eine Winkelhalbierende.--Lindi 88 19:43, 24. Okt. 2011 (CEST)

