Lösung von Aufgabe 8.4 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt. | Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt. | ||
<br /><br /> | <br /><br /> | ||
| − | Vor.: Es sei AB eine Strecke und M der Mittelpunkt von AB< | + | Vor.: Es sei <math>\overline {AB}</math> eine Strecke und M der Mittelpunkt von <math>\overline {AB}</math><br /> |
| − | Beh.: Es existiert höchstens ein Mittelpunkt | + | Beh.: Es existiert höchstens ein Mittelpunkt<br /> |
| − | Ann.: Es existiert | + | Ann.: Es existiert <math>M_2</math> mit folgenden Eigenschaften: <math>M_2</math> ist Mittelpukt von <math>\overline {AB}</math> und <math>M_2</math> ungleich <math>M</math><br /><br /> |
Beweis: | Beweis: | ||
Version vom 14. Dezember 2011, 17:53 Uhr
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
Vor.: Es sei 
eine Strecke und M der Mittelpunkt von
Beh.: Es existiert höchstens ein Mittelpunkt
Ann.: Es existiert 
mit folgenden Eigenschaften: ist Mittelpukt von und ungleich 
Beweis:
| Schritt | Begründung |
|---|---|
| (1)zw.(A,M,B) | Vor., Def Mittelpunkt |
| (2)zw.(A,M2,B) | Ann. |
(3)  |
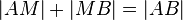(1),zw Relation |
(4)  |
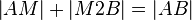(2), zw Relation |
(5) |
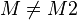Ann. |
(6)  |
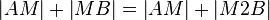(3),(4), Rechen in R |
(7)  |
Def. Mittelpunkt (3),(4) |
(8)  |
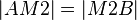Def. Mittelpunkt (3),(4) |
(9)  |
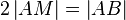(7) |
(10)  |
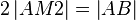(8) |
(11)  |
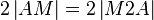(10) |
| (12) M=M2 | (11) Axiom vom Lineal |
Nicht alle Schritte kommen in einer Begründung vor. Also brauch man diese nicht, um zu Schritt 12 zu kommen. Was meint ihr?--Tutorin Anne 15:25, 7. Dez. 2011 (CET)
