Lösung Serie 08 - WiSe 2011/12: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) |
HecklF (Diskussion | Beiträge) |
||
| Zeile 16: | Zeile 16: | ||
# Konstruktion eines regelmäßigen Fünfecks mit der Einheitsstrecke als Seitenlänge:Formulieren Sie eine Konstruktionsbeschreibung zur Generierung eines solchen Fünfecks und begründen Sie diese. | # Konstruktion eines regelmäßigen Fünfecks mit der Einheitsstrecke als Seitenlänge:Formulieren Sie eine Konstruktionsbeschreibung zur Generierung eines solchen Fünfecks und begründen Sie diese. | ||
# Die Schüler wissen bereits, dass die Längen zweier Strecken <math>d</math> und <math>a</math> dann im Verhältnis des goldenen Schnittes zueinander stehen, wenn <math>\frac{d}{a}=\frac{1+\sqrt{5}}{2}</math> gilt. Eine Recherche im Internet ergibt, dass sich zwei Diagonalen des regelmäßigen Fünfecks im Verhältnis des goldenen Schnittes teilen. Maria meint: „Wenn das wahr ist, dann gilt für das regelmäßige Fünfeck auch, dass die Diagonalenlänge zur Seitenlänge im Verhältnis des goldenen Schnittes steht.“ Begründen Sie die Wahrheit von Marias Aussage. Sie können dabei auf eine Skizze Bezug nehmen.<br /> | # Die Schüler wissen bereits, dass die Längen zweier Strecken <math>d</math> und <math>a</math> dann im Verhältnis des goldenen Schnittes zueinander stehen, wenn <math>\frac{d}{a}=\frac{1+\sqrt{5}}{2}</math> gilt. Eine Recherche im Internet ergibt, dass sich zwei Diagonalen des regelmäßigen Fünfecks im Verhältnis des goldenen Schnittes teilen. Maria meint: „Wenn das wahr ist, dann gilt für das regelmäßige Fünfeck auch, dass die Diagonalenlänge zur Seitenlänge im Verhältnis des goldenen Schnittes steht.“ Begründen Sie die Wahrheit von Marias Aussage. Sie können dabei auf eine Skizze Bezug nehmen.<br /> | ||
| − | Dazu müsste zunächst bewiesen werden, dass jede Diagonale zu jeweils einer Seite des reg. Fünfecks parallel ist.<br /> | + | <br /> |
| + | Dazu müsste zunächst bewiesen werden, dass jede Diagonale zu jeweils einer Seite des reg. Fünfecks parallel ist. Dafür schicke ich ein Lemma voraus:<br /> | ||
| + | [[Datei:serie_08_a_2_1.jpg]] | ||
| + | <br /> | ||
| + | Im Anschluss daran beweise ich mit diesem Lemma die Vermutung Marias:<br /> | ||
| + | [[Datei:serie_08_a_2_2.jpg]] | ||
| + | <br /> | ||
| + | Auf der folgenden Seite finden sich weitere Skizzen und der erste 'Versuch' eines Beweises.<br /><br /> | ||
| + | [[Beweis_Versuch_Nummer_1_Serie_08_a_2]] | ||
| + | <br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 21:53, 18. Jan. 2012 (CET) | ||
Ich nehme Bezug auf den Apfel und das darin eingezeichnete reg. Fünfeck. In jedem regelmäßigen n-Eck gilt, dass die Innenwinkelsumme an jedem Eck gleich ist - (Begründung: trivial). <math>\overline{AE} \ kongruent \ \overline{BC} \ nach \ Voraussetzung \ reg. \ Fuenfeck.</math> Wir machen es uns nun einfacher und bestimmen den Mittelpunkt der Strecke <math>\overline{AB}</math>. Sei dieser M. Wenn wir nun die Mittelsenkrechte eintragen können wir zeigen, dass das Dreieck <math>\overline{MBC}</math> auf das Dreieck <math>\overline{MEA}</math> gespiegelt werden kann. Ich glaube es müsste aber noch einfacher gehen, seis drum. Begründungen sind Punkte A und B, sowie der Fixpunkt M und die beiden treuen Innenwinkel. Aufgrund der Spiegelunsdefinition existiert nun eine Senkrechte CE, die nach der Umkehrung des Stufenwinkelsatzes parallel zur Geraden AB ist. Für andere Diagonalen geht man analog vor, dies war o. B. d. A.<br /> | Ich nehme Bezug auf den Apfel und das darin eingezeichnete reg. Fünfeck. In jedem regelmäßigen n-Eck gilt, dass die Innenwinkelsumme an jedem Eck gleich ist - (Begründung: trivial). <math>\overline{AE} \ kongruent \ \overline{BC} \ nach \ Voraussetzung \ reg. \ Fuenfeck.</math> Wir machen es uns nun einfacher und bestimmen den Mittelpunkt der Strecke <math>\overline{AB}</math>. Sei dieser M. Wenn wir nun die Mittelsenkrechte eintragen können wir zeigen, dass das Dreieck <math>\overline{MBC}</math> auf das Dreieck <math>\overline{MEA}</math> gespiegelt werden kann. Ich glaube es müsste aber noch einfacher gehen, seis drum. Begründungen sind Punkte A und B, sowie der Fixpunkt M und die beiden treuen Innenwinkel. Aufgrund der Spiegelunsdefinition existiert nun eine Senkrechte CE, die nach der Umkehrung des Stufenwinkelsatzes parallel zur Geraden AB ist. Für andere Diagonalen geht man analog vor, dies war o. B. d. A.<br /> | ||
Hier doch noch eine Skizze:<br /> | Hier doch noch eine Skizze:<br /> | ||
Version vom 18. Januar 2012, 21:53 Uhr
„Interdisziplinäres Arbeiten ist das neue Schlagwort“, sagt Mathematiklehrerin Schultze-Kröttendörfer, „aber wie?“. Biologielehrer Krause, der schon „interdisziplinär“ arbeitete, als man noch „fächerübergreifend“ dazu sagte, gibt ihr einen Apfel: „In erster Näherung ist ein Apfel ein Rotationskörper. Lassen Sie die Schüler zur Rotationsachse senkrecht eine Schnittebene legen, welche den Apfel halbiert. Sie werden Erstaunliches entdecken können.“
„Oh, die Kernle bilden ä Fünfsternle“, freut sich Grundschullehrerin Sarah Plätscherbächle, die interessiert dem Gespräch gelauscht hat. „Nun ja“, räuspert sich Krause, „sagen wir ruhig Pentagramm dazu.“
„Aber zu dem Vieleck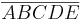 
dürfet man doch fünfseitiges Quadrat sage, oder?“, meint Sarah Plätscherbächle. „Nicht schlecht diese Idee“, antwortet Frau Schultze-Kröttendörfer, „man hat sich aber auf die Bezeichnung regelmäßiges Fünfeck geeinigt."
So präpariert geht Frau Schultze Kröttendörfer in ihren Unterricht, in dem die Schüler u.a. die folgenden Probleme lösen:
Na dann schauen wir mal, ob wir gute Schülerinnen und Schüler bei Frau Schultze Kröttendörfer wären.
- Fachliche Vorbetrachtung: Definieren Sie den Begriff regelmäßiges Fünfeck. Beachten Sie hierbei, dass in eine Definition nur das Nötigste bezüglich der Begriffsbestimmung aufgenommen wird.
Vorüberlegung: Ein regelmäßiges n-Eck zeichnet sich dadurch aus, dass die Streckenlängen kongruent sind. Wenn wir es zurückführen auf ein einfacheres Problem, so werden wir beim Dreieck kein Problem erkennen. Ein Dreieck mit drei gleich langen Seiten ist ein regelmäßiges Dreieck. Soweit so gut. Also wird das beim Fünfeck schon passen: Ein Fünfeck mit fünf gleich langen Seiten ist ein regelmäßiges Fünfeck - denkste. Wie komme ich darauf, dass das auch nicht der Fall sein kann? Naja ich führe wieder zurück auf ein einfacheres Problem: Das regelmäßige Viereck. Dies ist ja bekanntermaßen das Quadrat. Ein Viereck mit vier gleich langen Seiten ist aber auch die Raute und das ist nur in einem speziellen Falle ein Quadrat - nämlich, wenn es einen rechten Winkel hat. Also brauchen wir noch eine zusätzliche Information. Was haben das regelmäßige Dreieck und das Quadrat gemeinsam? Naja wenn man sie um die Innenwinkelsumme eines Ecks dreht, dann liegen wieder Ecke auf Ecke. Das schreit aber nach einem Kreis und genau so ist es. Und da dies eine Äquivalenz ist, (ein gleich lange Seiten <=> Umkreis) brauchen wir die gleich langen Seiten auch nicht mehr:
Ein Fünfeck mit Umkreis ist ein regelmäßiges Fünfeck.--Flo60 17:33, 18. Jan. 2012 (CET)
- Konstruktion eines regelmäßigen Fünfecks mit der Einheitsstrecke als Seitenlänge:Formulieren Sie eine Konstruktionsbeschreibung zur Generierung eines solchen Fünfecks und begründen Sie diese.
- Die Schüler wissen bereits, dass die Längen zweier Strecken
und 
dann im Verhältnis des goldenen Schnittes zueinander stehen, wenn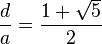 
gilt. Eine Recherche im Internet ergibt, dass sich zwei Diagonalen des regelmäßigen Fünfecks im Verhältnis des goldenen Schnittes teilen. Maria meint: „Wenn das wahr ist, dann gilt für das regelmäßige Fünfeck auch, dass die Diagonalenlänge zur Seitenlänge im Verhältnis des goldenen Schnittes steht.“ Begründen Sie die Wahrheit von Marias Aussage. Sie können dabei auf eine Skizze Bezug nehmen.
Dazu müsste zunächst bewiesen werden, dass jede Diagonale zu jeweils einer Seite des reg. Fünfecks parallel ist. Dafür schicke ich ein Lemma voraus:
Im Anschluss daran beweise ich mit diesem Lemma die Vermutung Marias:
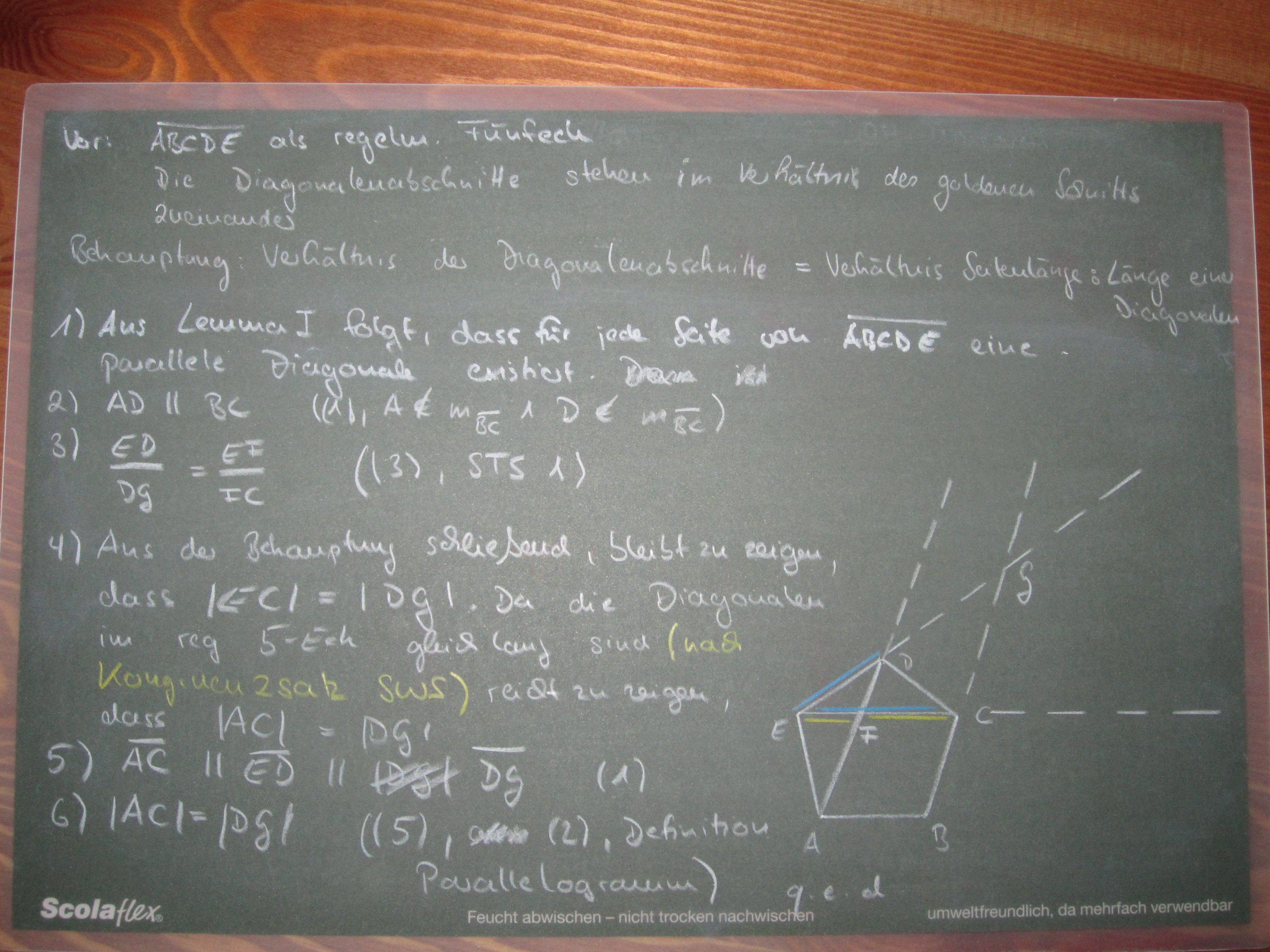
Auf der folgenden Seite finden sich weitere Skizzen und der erste 'Versuch' eines Beweises.
Beweis_Versuch_Nummer_1_Serie_08_a_2
--Flo60 21:53, 18. Jan. 2012 (CET)
Ich nehme Bezug auf den Apfel und das darin eingezeichnete reg. Fünfeck. In jedem regelmäßigen n-Eck gilt, dass die Innenwinkelsumme an jedem Eck gleich ist - (Begründung: trivial).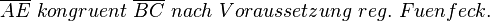 
Wir machen es uns nun einfacher und bestimmen den Mittelpunkt der Strecke 
. Sei dieser M. Wenn wir nun die Mittelsenkrechte eintragen können wir zeigen, dass das Dreieck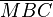 
auf das Dreieck 
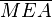gespiegelt werden kann. Ich glaube es müsste aber noch einfacher gehen, seis drum. Begründungen sind Punkte A und B, sowie der Fixpunkt M und die beiden treuen Innenwinkel. Aufgrund der Spiegelunsdefinition existiert nun eine Senkrechte CE, die nach der Umkehrung des Stufenwinkelsatzes parallel zur Geraden AB ist. Für andere Diagonalen geht man analog vor, dies war o. B. d. A.
Hier doch noch eine Skizze:
Jetzt aber zum eigentlichen Beweis. Auch hier gilt wieder oBdA. Aber hier gibt es zunächst die Skizze, sonst verenne ich mich wieder.
Um dies zu zeigen, muss nun gezeigt werden, dass A an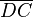 
gespiegelt wurde. Mit dem Prinzip des Ausfallwinkel gleich Einfallwinkel sollte uns das ohne Probleme gelingen: Geht nicht!
VIEL EINFACHER: Ich habe vorher ja so ungefähr bewiesen, dass die Seiten eine parallele Diagonale haben und zwar diejenige, deren Endpunkte nicht durch die Mittelsenkrechte der Seite gehen. Im Falle meiner Seite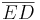 
ist dies die Diagonale 
. Nun gilt: Fehler beim Parsen(Lexikalischer Fehler): \overline{DF} \ || \ \overline{AC} \ und \ weil \ AD \ und BC \ ebenfalls \ parallel \ sind \ ist \overline{ACFD} \ ein \ Parallelogramm \ in \ dem \ gegenüberliegende \ Seiten \ logischerweise \ gleich \ lang \ sind \ und \ daraus \ folgt: \overline{AC} \tilde {=} \overline{DF}
FERTIG!--Flo60 18:53, 18. Jan. 2012 (CET)
- Mark ist von dem Zusammenspiel des Fünfecks mit dem eingefassten Pentagramm begeistert und beginnt zu experimentieren (s. untenstehende Skizze).Offenbar hätte er das Fünfeck
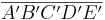auch durch zentrische Streckung vo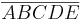n an 
konstruieren können. Bestimmen Sie den Streckfaktor dieser zentrischen Streckung. Hinweise: Sie dürfen das Verhältnis des goldenen Schnittes hinsichtlich Diagonalen- und Seitenlängen im regelmäßigen Fünfeck voraussetzen. (Die Suche nach geeigneten Strahlensatzfiguren kann bei der Lösung des Problems hilfreich sein.)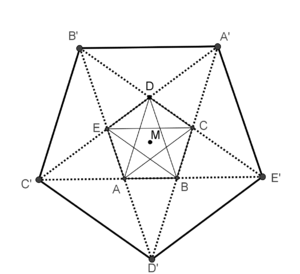
- Beweisen Sie, dass für die Seitenlänge und die Diagonalenlänge eines regelmäßigen Fünfecks wirklich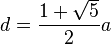
gilt.
- Die Idee von Sarah Plätscherbächle mit dem fünfseitigen Quadrat ist nicht schlecht. Wie beim Quadrat ist der Flächeninhalt des regelmäßigen Fünfecks proportional zum Quadrat der Seitenlänge . Formulieren und beweisen Sie einen „Satz des Pythagoras“ entsprechend der untenstehenden Skizze. Den üblichen Satz des Pythagoras dürfen Sie als bewiesen voraussetzen.
