Lösung Serie 08 - WiSe 2011/12
„Interdisziplinäres Arbeiten ist das neue Schlagwort“, sagt Mathematiklehrerin Schultze-Kröttendörfer, „aber wie?“. Biologielehrer Krause, der schon „interdisziplinär“ arbeitete, als man noch „fächerübergreifend“ dazu sagte, gibt ihr einen Apfel: „In erster Näherung ist ein Apfel ein Rotationskörper. Lassen Sie die Schüler zur Rotationsachse senkrecht eine Schnittebene legen, welche den Apfel halbiert. Sie werden Erstaunliches entdecken können.“
„Oh, die Kernle bilden ä Fünfsternle“, freut sich Grundschullehrerin Sarah Plätscherbächle, die interessiert dem Gespräch gelauscht hat. „Nun ja“, räuspert sich Krause, „sagen wir ruhig Pentagramm dazu.“
„Aber zu dem Vieleck 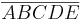 dürfet man doch fünfseitiges Quadrat sage, oder?“, meint Sarah Plätscherbächle. „Nicht schlecht diese Idee“, antwortet Frau Schultze-Kröttendörfer, „man hat sich aber auf die Bezeichnung regelmäßiges Fünfeck geeinigt."
dürfet man doch fünfseitiges Quadrat sage, oder?“, meint Sarah Plätscherbächle. „Nicht schlecht diese Idee“, antwortet Frau Schultze-Kröttendörfer, „man hat sich aber auf die Bezeichnung regelmäßiges Fünfeck geeinigt."
So präpariert geht Frau Schultze Kröttendörfer in ihren Unterricht, in dem die Schüler u.a. die folgenden Probleme lösen:
Na dann schauen wir mal, ob wir gute Schülerinnen und Schüler bei Frau Schultze Kröttendörfer wären.
Inhaltsverzeichnis |
Aufgabe 1
Fachliche Vorbetrachtung: Definieren Sie den Begriff regelmäßiges Fünfeck. Beachten Sie hierbei, dass in eine Definition nur das Nötigste bezüglich der Begriffsbestimmung aufgenommen wird.
Vorüberlegung: Ein regelmäßiges n-Eck zeichnet sich dadurch aus, dass die Streckenlängen kongruent sind. Wenn wir es zurückführen auf ein einfacheres Problem, so werden wir beim Dreieck kein Problem erkennen. Ein Dreieck mit drei gleich langen Seiten ist ein regelmäßiges Dreieck. Soweit so gut. Also wird das beim Fünfeck schon passen: Ein Fünfeck mit fünf gleich langen Seiten ist ein regelmäßiges Fünfeck - denkste. Wie komme ich darauf, dass das auch nicht der Fall sein kann? Naja ich führe wieder zurück auf ein einfacheres Problem: Das regelmäßige Viereck. Dies ist ja bekanntermaßen das Quadrat. Ein Viereck mit vier gleich langen Seiten ist aber auch die Raute und das ist nur in einem speziellen Falle ein Quadrat - nämlich, wenn es einen rechten Winkel hat. Also brauchen wir noch eine zusätzliche Information. Was haben das regelmäßige Dreieck und das Quadrat gemeinsam? Naja wenn man sie um die Innenwinkelsumme eines Ecks dreht, dann liegen wieder Ecke auf Ecke. Das schreit aber nach einem Kreis und genau so ist es. Und da dies eine Äquivalenz ist, (ein gleich lange Seiten <=> Umkreis) brauchen wir die gleich langen Seiten auch nicht mehr:
Ein Fünfeck mit Umkreis ist ein regelmäßiges Fünfeck.--Flo60 17:33, 18. Jan. 2012 (CET)
Ich würde folgendes definieren (geht in die gleiche Richtung):
Es seien ein Punkt  , ein Kreis
, ein Kreis  um
um  mit dem Radius
mit dem Radius  und
und 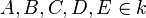 .
.
Für 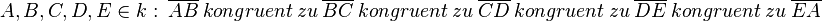 .
.
Pipi Langsocke 12:29, 20. Jan. 2012 (CET)
Aufgabe 2
Konstruktion eines regelmäßigen Fünfecks mit der Einheitsstrecke als Seitenlänge:Formulieren Sie eine Konstruktionsbeschreibung zur Generierung eines solchen Fünfecks und begründen Sie diese.
Aufgabe 3
Die Schüler wissen bereits, dass die Längen zweier Strecken  und
und  dann im Verhältnis des goldenen Schnittes zueinander stehen, wenn
dann im Verhältnis des goldenen Schnittes zueinander stehen, wenn 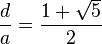 gilt. Eine Recherche im Internet ergibt, dass sich zwei Diagonalen des regelmäßigen Fünfecks im Verhältnis des goldenen Schnittes teilen. Maria meint: „Wenn das wahr ist, dann gilt für das regelmäßige Fünfeck auch, dass die Diagonalenlänge zur Seitenlänge im Verhältnis des goldenen Schnittes steht.“ Begründen Sie die Wahrheit von Marias Aussage. Sie können dabei auf eine Skizze Bezug nehmen.
gilt. Eine Recherche im Internet ergibt, dass sich zwei Diagonalen des regelmäßigen Fünfecks im Verhältnis des goldenen Schnittes teilen. Maria meint: „Wenn das wahr ist, dann gilt für das regelmäßige Fünfeck auch, dass die Diagonalenlänge zur Seitenlänge im Verhältnis des goldenen Schnittes steht.“ Begründen Sie die Wahrheit von Marias Aussage. Sie können dabei auf eine Skizze Bezug nehmen.
Dazu müsste zunächst bewiesen werden, dass jede Diagonale zu jeweils einer Seite des reg. Fünfecks parallel ist. Dafür schicke ich ein Lemma voraus:

Im Anschluss daran beweise ich mit diesem Lemma die Vermutung Marias:
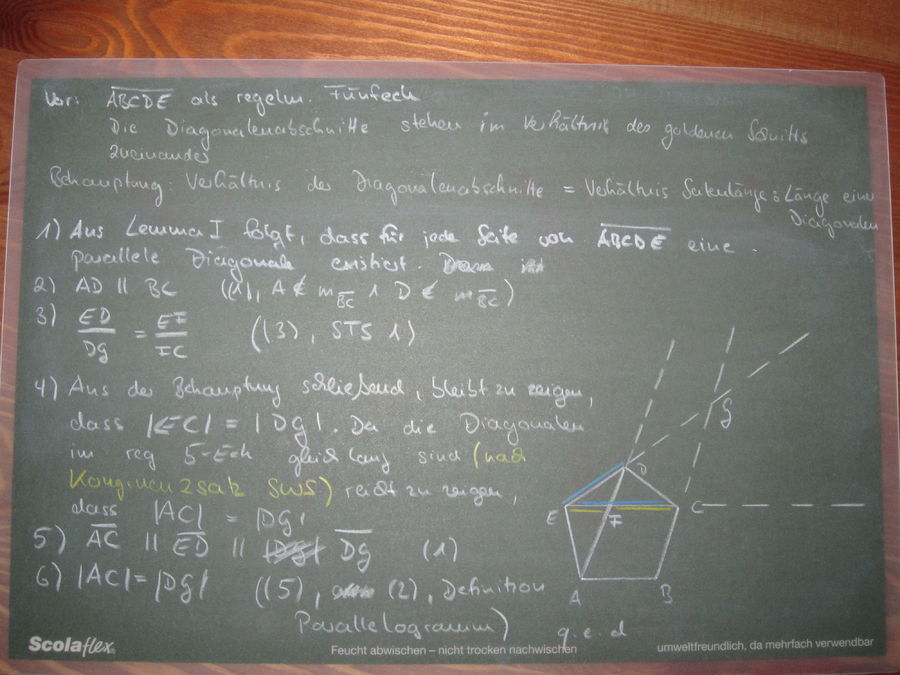
Auf der folgenden Seite finden sich weitere Skizzen und der erste 'Versuch' eines Beweises.
Beweis_Versuch_Nummer_1_Serie_08_a_2
--Flo60 21:53, 18. Jan. 2012 (CET)
Aufgabe 4
Mark ist von dem Zusammenspiel des Fünfecks mit dem eingefassten Pentagramm begeistert und beginnt zu experimentieren (s. untenstehende Skizze).Offenbar hätte er das Fünfeck 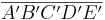 auch durch zentrische Streckung von
auch durch zentrische Streckung von 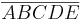 an
an  konstruieren können. Bestimmen Sie den Streckfaktor dieser zentrischen Streckung. Hinweise: Sie dürfen das Verhältnis des goldenen Schnittes hinsichtlich Diagonalen- und Seitenlängen im regelmäßigen Fünfeck voraussetzen. (Die Suche nach geeigneten Strahlensatzfiguren kann bei der Lösung des Problems hilfreich sein.)
konstruieren können. Bestimmen Sie den Streckfaktor dieser zentrischen Streckung. Hinweise: Sie dürfen das Verhältnis des goldenen Schnittes hinsichtlich Diagonalen- und Seitenlängen im regelmäßigen Fünfeck voraussetzen. (Die Suche nach geeigneten Strahlensatzfiguren kann bei der Lösung des Problems hilfreich sein.)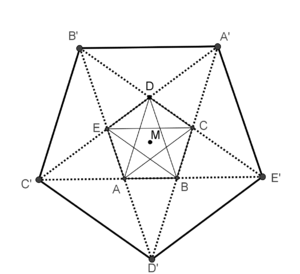
Aufgabe 5
Beweisen Sie, dass für die Seitenlänge  und die Diagonalenlänge
und die Diagonalenlänge  eines regelmäßigen Fünfecks wirklich
eines regelmäßigen Fünfecks wirklich 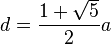 gilt.
gilt.
Aufgabe 6
Die Idee von Sarah Plätscherbächle mit dem fünfseitigen Quadrat ist nicht schlecht. Wie beim Quadrat ist der Flächeninhalt des regelmäßigen Fünfecks proportional zum Quadrat der Seitenlänge  . Formulieren und beweisen Sie einen „Satz des Pythagoras“ entsprechend der untenstehenden Skizze. Den üblichen Satz des Pythagoras dürfen Sie als bewiesen voraussetzen.
. Formulieren und beweisen Sie einen „Satz des Pythagoras“ entsprechend der untenstehenden Skizze. Den üblichen Satz des Pythagoras dürfen Sie als bewiesen voraussetzen.
Lösungsidee
Skizze
Beweis
Eigentlich löse ich die Aufgabe lediglich aus Freude darüber, herausgefunden zu haben, wie es denn funktionieren kann :-). Grundlegende Idee ist nämlich bereits in der Grundschuldidaktik zu finden: Flächeninhalte sind identisch, wenn sie deckungsgleich, zerlegungsgleich oder auslegungsgleich sind (vgl. Franke 2007). Letzteres suggeriert oftmals das Auslegen mit sog. Einheitsquadraten. Das funktioniert allerdinngs bei unserem Fünfeck mittelgut. Wenn wir uns von der Idee mit den Einheitsquadraten verabschieden und stattdessen Dreiecke zum Auslegen verwenden könnte es funktionieren. Das scheint vor allem deshalb sinnvoll, da man jede Fläche in Dreiecke teilen kann. Schwierig ist an der Aufgabe nur, dass wir bereits in den vorherigen Schritten derart mit Dreiecken gearbeitet haben (bedingt durch die Diagonalen), dass man jetzt den Wald vor lauter Bäumen nicht mehr sieht. Heißt nichts anderes: Welche Dreiecke bringen uns schlussendlich eigentlich zum Ziel?
Obige Skizze versucht es zu verdeutlichen. Wir wissen bereits, dass jedes regelmäßige n-Eck einen Umkreis besitzt. Zudem ist (glücklicherweise) der Satz des Pythagoras bereits vorausgesetzt. Nun können wir uns das Fünfeck in fünf kongruente Teildreiecke derart zerlegen, wie in der Skizze angezeigt ist. Über SSS wird relativ schnell klar, dass die fünf Dreiecke kongruent zueinander sind (da F Mittelpunkt des Umkreises und Fünfeck regelmäßig). Durch diese Eigenschaft wissen wir auch, dass die Winkel um F in jedem der Dreiecke kongruent zueinander sind.
Nun legen wir ein Lot von F auf o. B. d. A.  . Der Radius des Kreises k sei mit r bezeichnet. Für dieses Lot gilt nun folgende Länge:
. Der Radius des Kreises k sei mit r bezeichnet. Für dieses Lot gilt nun folgende Länge: 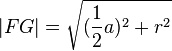 .
.
Der Flächeninhalt für unser Fünfeck 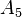 lässt sich nun folgendermaßen berechnen:
lässt sich nun folgendermaßen berechnen: 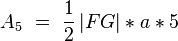
Wir haben nun folgendes gezeigt: Wir haben gezeigt, dass man die Höhe der Teildreiecke mit Pythagoras berechnent kann (dass die beiden kleineren Teildreiecke 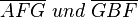 kongruent zueinander sind folgt aus SSS oder anderen Kongreuenzsätzen. Wir können mittels Innenwinkel eines Teildreiecks
kongruent zueinander sind folgt aus SSS oder anderen Kongreuenzsätzen. Wir können mittels Innenwinkel eines Teildreiecks 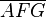 und dem
und dem 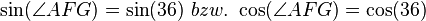 den Radius r in Abghängigkeit bekannter Längen angeben aber das bringt uns nun nicht mehr näher an das Ziel, das vor unseren Augen liegt. Da wir nun alles gezeigt haben, was wir folgend verwenden wollen, können wir nun folgende Vereinfachung treffen:
den Radius r in Abghängigkeit bekannter Längen angeben aber das bringt uns nun nicht mehr näher an das Ziel, das vor unseren Augen liegt. Da wir nun alles gezeigt haben, was wir folgend verwenden wollen, können wir nun folgende Vereinfachung treffen: 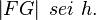 . Nun gilt für unseren Flächeninhalt folgendes:
. Nun gilt für unseren Flächeninhalt folgendes: 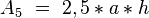 .
.
Nun gilt 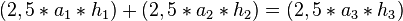 oder um auf den Satz des Pythagoras etwas genauer zurück zu kommen sogar mit Quadraten:
oder um auf den Satz des Pythagoras etwas genauer zurück zu kommen sogar mit Quadraten: 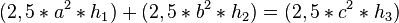
Und warum das so ist, seht ihr nach der nächsten Maus :-) --Flo60 12:19, 10. Jun. 2012 (CEST)
'Nach der nächsten Maus'
Wir haben in der Voraussetzung, dass der 'Flächeninhalt des regelmäßigen Fünfecks proportional zum Quadrat der Seitenlänge  ' ist. Was bedeutet das? Machen wir uns dies anhand eines Beispiels klar:
' ist. Was bedeutet das? Machen wir uns dies anhand eines Beispiels klar:
| a | 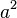 |
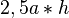 |
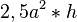
|
|---|---|---|---|
| 1 | 1 | 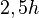 |
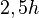
|
| 2 | 4 | 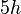 |
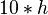
|
| 3 | 9 | 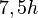 |
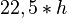
|
Was heißt das nun abstrakt: 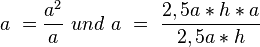 . Nun folgt daraus folgendes und nichts anderes: Wenn der Satz des Pytagoras lautet: a² + b² = c² gilt auch
. Nun folgt daraus folgendes und nichts anderes: Wenn der Satz des Pytagoras lautet: a² + b² = c² gilt auch 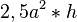 +
+ 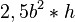 =
= 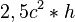 --Flo60 12:53, 10. Jun. 2012 (CEST)
--Flo60 12:53, 10. Jun. 2012 (CEST)
Und weil das hier alles mehr oder weniger großer Quatsch ist und ich mit dem zeugs hier mal sowas von nicht zufrieden bin, kommt hier der '5-Minuten-Prüfungs-Turbo' :-)
5-Minuten-Prüfungs-Turbo
Ohne das ganze vorgeplenkel von vorhin können wir mit Verweis auf die Skizze angeben, dass der Flächeninhalt von unserem Fünfeck 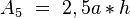 ist.
ist.
Nun wissen wir, dass alle regelmäßigen Fünfecke zueinander ähnlich sind. Es gilt demnach folgendes: 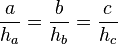 .
.
Nun kann ich ja aus jucks und tollerrei mal Behaupten (was ich oben unbegründeterweise gemacht habe), dass 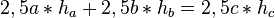 ist. Wir beweisen wie folgt direkt.
ist. Wir beweisen wie folgt direkt.
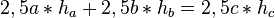
Dies dividieren wir durch 2,5 und es bleibt: 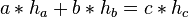 .
Weil nun gilt, dass die Seiten und die Höhen ähnlich sind, kann ich mit
.
Weil nun gilt, dass die Seiten und die Höhen ähnlich sind, kann ich mit 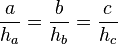 multiplizieren und erhalte:
multiplizieren und erhalte: 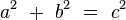
Und weil der gilt bin ich fertig - SOOOOOO EINFACH WÄRS GEWESEN ÄÄÄÄÄHHHHHHHH!!!!!! - und in 5 Minuten tatsächlich schaffbar :-(. --Flo60 13:46, 10. Jun. 2012 (CEST)