Serie 5 (WS 12 13): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.1) |
||
| Zeile 12: | Zeile 12: | ||
==Aufgabe 5.1== | ==Aufgabe 5.1== | ||
Begründen Sie: | Begründen Sie: | ||
| − | #Jedes Modell für die Inzidenzaxiome der Ebene beinhaltet wenigstens 3 | + | #Jedes Modell für die Inzidenzaxiome der Ebene beinhaltet wenigstens 3 Punkte. |
| − | #Jedes Modell für die Inzidenzaxiome des Raumes beinhaltet wenigstens | + | #Jedes Modell für die Inzidenzaxiome des Raumes beinhaltet wenigstens 4 Punkte. |
<br /> | <br /> | ||
[[Lösung von Aufgabe 5.1_S (WS_12_13)]] | [[Lösung von Aufgabe 5.1_S (WS_12_13)]] | ||
Version vom 24. November 2012, 15:01 Uhr
|
weitere Aufgaben zur Inzidenz„Man muß jederzeit an Stelle von ‚Punkten‘, ‚Geraden‘, ‚Ebenen‘, ‚Tische‘, ‚Stühle‘, ‚Bierseidel‘ sagen
können.“ Aufgabe 5.1Begründen Sie:
Aufgabe 5.2Gegeben seien eine rote Kugel aus Knete (
Die Inzidenzrelation interpretieren wir wie folgt: Ein Modellpunkt inziert mit einer Modellgeraden, wenn der Modellpunkt auf die Modellgerade gesteckt wurde.
Lösung von Aufgabe 5.2_S (WS_12_13) Aufgabe 5.3Definition Zwei Geraden sind komplanar, wenn es eine Ebene gibt, die beide Geraden vollständig enthält. Beweisen Sie den folgenden Satz:
Aufgabe 5.4Formulieren Sie Kontraposition und die Umkehrung von Satz * aus der Aufgabe 5.3. Äußern Sie sich zum Wahrheitgehalt dieser beiden Implikationen. Begründen Sie Ihre Äußerungen. Lösung von Aufgabe 5.4_S (WS_12_13) Aufgabe 5.5Begründen Sie: Aufgabe 5.6Axiom I.7 liefert 4 Punkte, die nicht komplanar sind.
Lösung von Aufg. 5.6_S (WS_12_13)
|
 ), eine blaue Kugel aus Knete (
), eine blaue Kugel aus Knete ( ), eine grüne Kugel aus Knete (
), eine grüne Kugel aus Knete ( ) und eine schwarze Kugel aus Knete (
) und eine schwarze Kugel aus Knete ( ). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.
). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.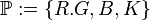
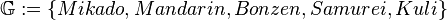
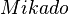
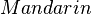
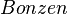
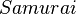
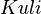
 und
und  genau einen Schnittpunkt haben, so sind sie komplanar.
genau einen Schnittpunkt haben, so sind sie komplanar.
 macht nur Sinn, wenn
macht nur Sinn, wenn 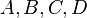 diese 4 Punkte.
diese 4 Punkte. eine Ebene mit
eine Ebene mit 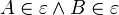 .
. mit
mit 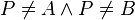 .
.
