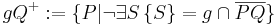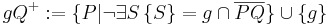Halbebenen oder das Axiom von Pasch: Unterschied zwischen den Versionen
TimoRR (Diskussion | Beiträge) (→Definition IV.2: (Halbebene)) |
(→Definition IV.2: (Halbebene)) |
||
| Zeile 120: | Zeile 120: | ||
HI, schau mal, ich hab das abgeändert, aber kann man das so stehen lassen!? | HI, schau mal, ich hab das abgeändert, aber kann man das so stehen lassen!? | ||
also einfach nur g in der Lösungsmenge!? Oder muss das irgendwie mit {P Element von g} oder wie wäre das formal korrekt?--[[Benutzer:TimoRR|TimoRR]] 22:04, 21. Jun. 2010 (UTC) | also einfach nur g in der Lösungsmenge!? Oder muss das irgendwie mit {P Element von g} oder wie wäre das formal korrekt?--[[Benutzer:TimoRR|TimoRR]] 22:04, 21. Jun. 2010 (UTC) | ||
| + | |||
| + | Das müsste so OK sein, die Halbebene gQ+ ist ja die Vereingung genau dieser zwei Punktmengen... | ||
| + | Danke :) | ||
== Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen == | == Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen == | ||
Version vom 21. Juni 2010, 23:12 Uhr
Inhaltsverzeichnis
|
Halbebenen und das Axiom von Pasch
Halbebenen
Analogiebetrachtungen
| |
|
 , das in Klassen eingeteilt wird , das in Klassen eingeteilt wird | |
 ist eine Gerade ist eine Gerade
|
 ist eine Gerade ist eine Gerade
|
 | |
| Punktmenge | Punktmenge |
 , das , das  in Klassen einteilt in Klassen einteilt | |
| Halbgerade | Halbebene |
 | |
| Teilmenge | Teilmenge |
 teilt teilt  in genau zwei Klassen in genau zwei Klassen | |
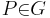 , die mit , die mit  bezüglich bezüglich  „auf derselben Seite liegen“ „auf derselben Seite liegen“ | |
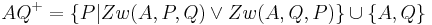
|
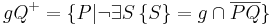
|
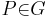 , die bezüglich , die bezüglich  nicht auf der Seite von nicht auf der Seite von  liegen. liegen. | |
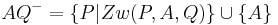
|
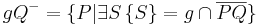
|
BITTE ÜBERPRÜFEN --TimoRR 20:14, 16. Jun. 2010 (UTC)
Bemerkungen zu den Analogieüberlegungen --*m.g.* 19:18, 17. Jun. 2010 (UTC)
- Wird in beiden Fällen wirklich eine Gerade in Klassen eingeteilt? Erhalten wir eine Halbebene dadurch, dass wir eine Gerade in Klassen einteilen?
- Dimension: Gemeint ist, welche Dimension das Objekt hat, welches in Klassen bzw. Teilmengen eingeteilt wird. Ein räumliches Objekt, wie etwa ein Würfel hat die Dimension drei, ein Quadrat liegt vollständig in einer Ebene und ist deshalb ein zweidimensionales Objekt. Eine Strecke liegt auf einer Geraden und ist deshalb ein eindimensionales geometrisches Objekt. Wir haben es bei unseren beiden Begriffen Halbgerade und Halbebene einmal mit einem 1D- und einmal mit einem 2D-Begriff zu tun. Den Begriff der Dimension verwenden wir hier intuitiv, ohne ihn definiert zu haben.
- Halbgerade: Eine Gerade wird in zwei Halbgeraden eingeteilt. Was für ein Objekt bewirkt diese Einteilung? Eine Halbgerade oder nicht doch eher ein Punkt, der Anfangspunkt der beiden Halbgeraden? Eine Ebene läßt ich auf unendlich viele Arten in genau zwei Halbenen zerlegen. Was für ein Objekt ist verantwortlich dafür, dass wir eine Einteilung in zwei spezielle Halbebenen bekommen? Was ist das Analogon zum Anfangspunkt zweier entgegengesetzter Strahlen bezüglich der Einteilung einer Ebene in zwei Halbebene, deren Vereinigungsmenge wieder die Ausgangebene ergibt?
- Die Definitionen zu den beiden Halbgeraden
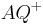 und
und 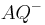 sind korrekt. Die Analogie zum problem der Halbebenen wird aber besser verdeutlich, wenn man diese Definitionen anders formuliert und sich dabei explizit auf die Strecke
sind korrekt. Die Analogie zum problem der Halbebenen wird aber besser verdeutlich, wenn man diese Definitionen anders formuliert und sich dabei explizit auf die Strecke 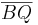 bezieht. Die Idee, Halbgeraden über die Strecke
bezieht. Die Idee, Halbgeraden über die Strecke  zu definieren lag der Übungsaufgabe 7.4 Lösung_von_Aufgabe_7.4 zugrunde. Die Definition habe ich zu Beginn meiner Vorlesung vom 11.06. erläutert.
zu definieren lag der Übungsaufgabe 7.4 Lösung_von_Aufgabe_7.4 zugrunde. Die Definition habe ich zu Beginn meiner Vorlesung vom 11.06. erläutert.
- Die Definition der Halbebenen ist prinzipiell richtig. Nach stillschweigender Konvention kennzeichnen wir jedoch Punkte durch große lateinische Buchstaben. Also nicht
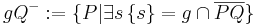 sondern
sondern 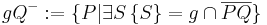 CHECK
CHECK
Definition des Begriffs der Halbebene
Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen
Offene Halbebenen
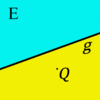
Die beiden Seiten, in die die Menge der Punkte einer Ebene  , die nicht auf einer Geraden
, die nicht auf einer Geraden  dieser Ebene liegen, durch diese Gerade
dieser Ebene liegen, durch diese Gerade  eingeteilt wird, heißen offene Halbebenen von
eingeteilt wird, heißen offene Halbebenen von  bezüglich der Trägergeraden
bezüglich der Trägergeraden  . Der nicht zu
. Der nicht zu  gehörende Referenzpunkt
gehörende Referenzpunkt 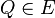 bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich
bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich  mit
mit  auf derselben Seite liegen, wird mit
auf derselben Seite liegen, wird mit  bezeichnet, die andere offene Halbebene von
bezeichnet, die andere offene Halbebene von  bezüglich
bezüglich  und
und  mit
mit  .
.
Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was es denn darunter zu verstehen wäre, dass zwei Punkte  und
und  einer Ebene
einer Ebene  auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden
auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden  liegen.
liegen.
Definition IV.1: (offene Halbebene)
- Es sei
 eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Punktmengen:
versteht man die folgenden Punktmengen:
- Es sei
Ich bin mir nicht sicher ob ich hiermit richtig liege, aber ist bei gQ- nach dieser Definition nicht auch die Punktmenge der Geraden g mit dabei, denn wenn P auf g liegen würde, gäbe es auch eine Schnittpunkt S, mit S=P oder? gQ- wäre also die Definition einer geschlossenen Halbebene..
--Principella 20:31, 21. Jun. 2010 (UTC)
Hhm - Gute Frage =) Ich denke, wir haben schon von vornherein per Definition ausgeschlossen, dass P ein Element von g ist, sondern in einer Ebene entweder mit Q oder in der anderen von Q liegt... Vlt sollten wir in der Definition IV.1 das ergänzen, dass Q UND P in der Ebene E liegen, aber nicht zur Geraden g gehören!?? Erst bei der (geschlossenen) Halbebene wird die Menge aller Punkte von g mit gQ+ oder gQ- vereint. Bei der offenen Halbebene gibt es dann keine Vereinigung, sondern nur den einen Schnittpunkt mit g, um zu zeigen, dass es eine andere Ebene ist, nämlich gQ- (also g ohne den Punkt Q)... --TimoRR 21:11, 21. Jun. 2010 (UTC)
- m.g.*, können Sie uns Helfen und das klären ;-)
Ich glaub "P nicht Element g" muss einfach mit in die Definition rein, hab aber keine Ahnung wie das geht... --Principella 21:22, 21. Jun. 2010 (UTC)
Halbebenen
Vereinigt man die Menge der Punkte einer offenen Halbeben mit der Menge der Punkte der Trägergerade so erhält man eine Halbebene.
Definition IV.2: (Halbebene)
--Principella 20:30, 21. Jun. 2010 (UTC)
HI, schau mal, ich hab das abgeändert, aber kann man das so stehen lassen!? also einfach nur g in der Lösungsmenge!? Oder muss das irgendwie mit {P Element von g} oder wie wäre das formal korrekt?--TimoRR 22:04, 21. Jun. 2010 (UTC)
Das müsste so OK sein, die Halbebene gQ+ ist ja die Vereingung genau dieser zwei Punktmengen... Danke :)
Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen
Repräsentantenunabhängigkeit?
Satz IV.1
- Wenn
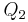 ein Punkt der Halbebene
ein Punkt der Halbebene 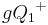 ist, dann gilt
ist, dann gilt 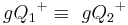 und
und  .
.
- Wenn
Beweis des Satzes IV.1
Fehlanzeige
Das Axiom von Pasch
- Was Axiomatik ist und wie man Axiome zu formulieren hat, das ist erst gegen Ende des 19. Jh. von Pasch gezeigt worden; von ihm lernten es die italienischen Geometer und lernte es Hilbert.
Hans Freudenthal, Mathematik als pädagogische Aufgabe, Stuttgart 1973, S. 14)
- Was Axiomatik ist und wie man Axiome zu formulieren hat, das ist erst gegen Ende des 19. Jh. von Pasch gezeigt worden; von ihm lernten es die italienischen Geometer und lernte es Hilbert.
Axiom III.2: Das Axiom von Pasch
- Gegeben sei ein Dreieck
 . Ferner sei
. Ferner sei  eine Gerade, die durch keinen der drei Eckpunkte
eine Gerade, die durch keinen der drei Eckpunkte  geht. Wenn
geht. Wenn  eine der drei Seiten des Dreiecks
eine der drei Seiten des Dreiecks  schneidet, dann schneidet
schneidet, dann schneidet  genau eine weitere Seite des Dreiecks
genau eine weitere Seite des Dreiecks  .
.
- Gegeben sei ein Dreieck
Konvexe Punktmengen
Definition IV.3: (konvexe Punktmenge)
- Eine Menge
 von Punkten heißt konvex, wenn mit je zwei Punkten
von Punkten heißt konvex, wenn mit je zwei Punkten  und
und  dieser Menge die gesamte Strecke
dieser Menge die gesamte Strecke  zu
zu  gehört.
gehört.
- Eine Menge
Satz IV.2
- Halbebenen sind konvexe Punktmengen
Beweis von Satz IV.2
trivial (Der Leser überzeuge sich davon)
Satz IV.3
- Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Beweis von Satz IV.3
Es seien  und
und 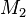 zwei konvexe Mengen.
zwei konvexe Mengen.
zu zeigen: Der Durchschnitt der beiden Mengen  und
und 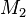 ist auch konvex.
ist auch konvex.
...
 gehört u.a., dass jede Gerade
gehört u.a., dass jede Gerade 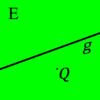
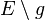 , die mit
, die mit