Serie 2 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.04 SoSe 2013) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.04 SoSe 2013) |
||
| Zeile 34: | Zeile 34: | ||
=Aufgabe 2.04 SoSe 2013= | =Aufgabe 2.04 SoSe 2013= | ||
Sie haben einen Klassensatz Heidelberger Winkelkreuze ([[Heidelberger_Winkelkreuz]]). | Sie haben einen Klassensatz Heidelberger Winkelkreuze ([[Heidelberger_Winkelkreuz]]). | ||
| − | Mit dem Heidelberger Winkelkreuz lassen Sie Ihre Schüler nur Parallelogramme spannen. Danach sollen eine Regel entwickeln, welche Stifte auf den Schenkeln des Kreuzes auszuwählen sind, damit ein Parallelogramm gespannt wird. | + | Mit dem Heidelberger Winkelkreuz lassen Sie Ihre Schüler nur Parallelogramme spannen. Danach sollen eine Regel entwickeln, welche Stifte auf den Schenkeln des Kreuzes auszuwählen sind, damit ein Parallelogramm gespannt wird. Sie dürfen davon ausgehen, dass die vier Schenkel des Kreuzes nummeriert sind und alle die Stifte, die denselben Abstand zum Drehpunkt des Kreuzes haben, mit derselben Farbe angestrichen wurden: Rot, Grün, Blau, Gelb (von innen nach außen). |
# Wie könnte diese Regel formuliert sein? | # Wie könnte diese Regel formuliert sein? | ||
# Formulieren Sie eine Definition des Begriffs Parallelogramm, der sich unmittelbar aus dieser Regel ergibt. | # Formulieren Sie eine Definition des Begriffs Parallelogramm, der sich unmittelbar aus dieser Regel ergibt. | ||
[[Lösung von Aufgabe 2.04 SoSe 2013 S]] | [[Lösung von Aufgabe 2.04 SoSe 2013 S]] | ||
| + | |||
=Aufgabe 2.05 SoSe 2013= | =Aufgabe 2.05 SoSe 2013= | ||
Version vom 27. April 2013, 11:56 Uhr
Inhaltsverzeichnis |
Die gesamte Serie zum Ausdrucken
Aufgabe 2.01 SoSe 2013
Ergänzen Sie die Lücken durch Verwendung von
- notwendig aber nicht hinreichend
- hinreichend aber nicht notwendig
- hinreichend
- notwenig
- notwendig und hinreichend.
Sollten mehrere diesbezügliche Auswahlmöglichkeiten bestehen, verwenden Sie die schärfste der möglichen Formulierungen.
- Dafür, dass
 die Summe
die Summe 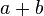 teilt, ist es ... , dass
teilt, ist es ... , dass  sowohl
sowohl  als auch
als auch teilt. (
teilt. (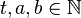 )
)
- Dafür, dass
 ein Rechteck ist, ist es ... , dass
ein Rechteck ist, ist es ... , dass 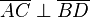 gilt.
gilt.
- Dafür, dass ein Dreieck
 rechtwinklig ist, ist es ... , dass kein Innenwinkel von
rechtwinklig ist, ist es ... , dass kein Innenwinkel von  größer als 90° ist.
größer als 90° ist.
- Dafür, dass ein Dreieck
 stumpfwinklig ist, ist es ... , dass ein Innenwinkel von
stumpfwinklig ist, ist es ... , dass ein Innenwinkel von  größer als 90° ist.
größer als 90° ist.
- Dafür, dass ein Dreieck rechtwinklig ist, ist es ... , dass der Mittelpunkt seines Umkreises der Mittelpunkt einer seiner Seiten ist.
- Dafür dass ein Viereck ein Rechteck ist, ist es ... , dass alle seine Seiten gleichlang sind.
- Dafür dass ein Viereck ein Rechteck ist, ist es ... , dass es einen rechten Innenwinkel hat und alle seine Seiten gleichlang sind.
Lösung von Aufgabe 2.02 SoSe 2013 S
Aufgabe 2.02 SoSe 2013
Unter einem Trapez wollen wir ein Viereck verstehe, das ein Paar zueinender paralleler Seiten hat. Es sei  ein Trapez. Formulieren Sie
ein Trapez. Formulieren Sie
- eine zwar hinreichende aber nicht notwendige Bedingung dafür, dass
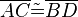 gilt,
gilt,
- eine hinreichende und notwendige Bedingung dafür, dass
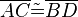 gilt,
gilt,
- eine notwendige aber nicht hinreichende Bedingung dafür, dass
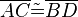 gilt,
gilt,
- ein Kriterium dafür, dass
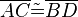 gilt.
gilt.
Lösung von Aufgabe 2.02 SoSe 2013 S
Aufgabe 2.03 SoSe 2013
Definieren Sie den Begriff Parallelogramm
- nur unter Verwendung der Eigenschaften der Seitenlängen von Parallelogrammen,
- unter Verwendung Semantik der Begriffsbezeichnung,
Lösung von Aufgabe 2.03 SoSe 2013 S
Aufgabe 2.04 SoSe 2013
Sie haben einen Klassensatz Heidelberger Winkelkreuze (Heidelberger_Winkelkreuz). Mit dem Heidelberger Winkelkreuz lassen Sie Ihre Schüler nur Parallelogramme spannen. Danach sollen eine Regel entwickeln, welche Stifte auf den Schenkeln des Kreuzes auszuwählen sind, damit ein Parallelogramm gespannt wird. Sie dürfen davon ausgehen, dass die vier Schenkel des Kreuzes nummeriert sind und alle die Stifte, die denselben Abstand zum Drehpunkt des Kreuzes haben, mit derselben Farbe angestrichen wurden: Rot, Grün, Blau, Gelb (von innen nach außen).
- Wie könnte diese Regel formuliert sein?
- Formulieren Sie eine Definition des Begriffs Parallelogramm, der sich unmittelbar aus dieser Regel ergibt.
Lösung von Aufgabe 2.04 SoSe 2013 S

