Lösung von Aufgabe 9.4P (SoSe 13): Unterschied zwischen den Versionen
| Zeile 16: | Zeile 16: | ||
<br /> | <br /> | ||
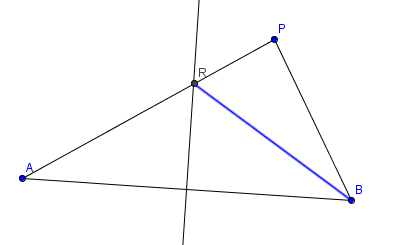
| + | [[Datei:9-4-Skizze.PNG ]]<br /> | ||
Betrachtung: Punkt P liegt in der selben Halbebene von m wie B | Betrachtung: Punkt P liegt in der selben Halbebene von m wie B | ||
| Zeile 45: | Zeile 46: | ||
Ich verstehe Schritt 6 nicht, denn der Abstand BP kommt ja in 5 nicht vor. Da sind noch Zwischenschritte nötig.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:13, 8. Jul. 2013 (CEST) | Ich verstehe Schritt 6 nicht, denn der Abstand BP kommt ja in 5 nicht vor. Da sind noch Zwischenschritte nötig.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:13, 8. Jul. 2013 (CEST) | ||
| − | + | * Da ich bei der Betrachtung oben geschrieben habe, dass mein Punkt P in der selben Halbebene von m wie B liegt, ergibt sich nach meiner Konstruktion ein neues "Dreieck" mit APB und ich will ja zeigen, dass die Strecke AP gleich Strecke BP ist. Durch Schritt 4 und 5 sehe ich, dass die Strecke AP kleiner ist als die Strecke BP und dass ist ein Wiederspruch zur Voraussetzung. Ich weis es ist kompliziert, da keine Zeichnung vorliegt. Ich kann irgendwie mein Bild nicht hochladen. Herr Schnirch, hatte uns in der Vorlesung eine Skizze gezeichnet, wo er das Dreieck einfach verlängert hat und wir dadurch 2 Dreiecke hatte. Ich weis aber nicht, wie ich es in Schritten erklären soll;-/---[[Benutzer:Blumenkind|Blumenkind]] 16:04, 8. Jul. 2013 (CEST)Blumenkind 16:03, 8.Juli | |
| − | + | **Ich habe die Idee schon verstanden und die Skizze kenne ich und habe sie jetzt nochmal zugefügt. Entscheident ist, dass trotzdem nicht so Schritt 6 abgeleitet werden kann. Das was du da über ein Dreieck schreibst, muss auch im Beweis stehen. (Sieh in der Aufgabenstellung bei TIPP).--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:13, 10. Jul. 2013 (CEST) | |
[[Kategorie: Einführung_P]] | [[Kategorie: Einführung_P]] | ||
Version vom 10. Juli 2013, 14:13 Uhr
m sei Mittelsenkrechte der Strecke  . Beweisen Sie durch Kontraposition:
. Beweisen Sie durch Kontraposition: 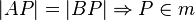
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.
Kontraposition lautet: P 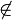 m
m IAPI
IAPI IBPI
IBPI
Wenn P nicht Element m ist, dann sind 2 Fälle zu betrachten. Weil P kann einmal in der Halbebene von m liegen in der B liegt oder P kann in der Halbebene von m liegen in der A liegt.
| Voraussetzung | AP|=|BP|, m ist Mittelsenkrechte der Strecke AB| |
| Behauptung | P ist Element m |
| Annahme | P ist nicht Element m |
Betrachtung: Punkt P liegt in der selben Halbebene von m wie B
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | (Strecke BP geschnitten mit m=leere Menge ) | (Def. HE, Annahme) |
| 2 | (Strecke AP geschnitten mit m =(R)) | (1,) |
| 3 | (R ist Element Strecke AP) | (2) |
| 4 | (Zw(ARP)) | (Def. ZW, 3) |
| 5 | IARI + IRPI= IAPI | 4 |
| ... | ... | ... |
| ... | ... | ... |
| 6 | StreckeAPI > IStrecke BPI | 5 |
WIEDERSPRUCH ZUR VORAUSSETZUNG. ANNAHME VERWERFEN, BEHAUPTUNG STIMMT.
--Blumenkind 17:49, 4. Jul. 2013 (CEST)BLUMENKIND 17:47, 4.JULI
Ich verstehe Schritt 6 nicht, denn der Abstand BP kommt ja in 5 nicht vor. Da sind noch Zwischenschritte nötig.--Tutorin Anne 14:13, 8. Jul. 2013 (CEST)
- Da ich bei der Betrachtung oben geschrieben habe, dass mein Punkt P in der selben Halbebene von m wie B liegt, ergibt sich nach meiner Konstruktion ein neues "Dreieck" mit APB und ich will ja zeigen, dass die Strecke AP gleich Strecke BP ist. Durch Schritt 4 und 5 sehe ich, dass die Strecke AP kleiner ist als die Strecke BP und dass ist ein Wiederspruch zur Voraussetzung. Ich weis es ist kompliziert, da keine Zeichnung vorliegt. Ich kann irgendwie mein Bild nicht hochladen. Herr Schnirch, hatte uns in der Vorlesung eine Skizze gezeichnet, wo er das Dreieck einfach verlängert hat und wir dadurch 2 Dreiecke hatte. Ich weis aber nicht, wie ich es in Schritten erklären soll;-/---Blumenkind 16:04, 8. Jul. 2013 (CEST)Blumenkind 16:03, 8.Juli
- Ich habe die Idee schon verstanden und die Skizze kenne ich und habe sie jetzt nochmal zugefügt. Entscheident ist, dass trotzdem nicht so Schritt 6 abgeleitet werden kann. Das was du da über ein Dreieck schreibst, muss auch im Beweis stehen. (Sieh in der Aufgabenstellung bei TIPP).--Tutorin Anne 15:13, 10. Jul. 2013 (CEST)