Lösung von Aufgabe 10.1: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
TimoRR (Diskussion | Beiträge) |
|||
| Zeile 2: | Zeile 2: | ||
::Eine Gerade <math>\ g</math> und eine Ebene <math>\epsilon</math> stehen senkrecht aueinander, wenn es in <math>\epsilon</math> <s>eine</s> ''mindestens zwei'' Geraden gibt, die vollständig in <math>\epsilon</math> liegen, und senkrecht auf <math>\ g</math> stehen. | ::Eine Gerade <math>\ g</math> und eine Ebene <math>\epsilon</math> stehen senkrecht aueinander, wenn es in <math>\epsilon</math> <s>eine</s> ''mindestens zwei'' Geraden gibt, die vollständig in <math>\epsilon</math> liegen, und senkrecht auf <math>\ g</math> stehen. | ||
| + | |||
| + | :::'''Nochmal richtig:''' Eine Gerade <math>\ g</math> und eine Ebene <math>\epsilon</math> stehen senkrecht aufeinander, wenn es in <math>\epsilon</math> zwei sich schneidende Geraden gibt, die senkrecht auf <math>\ g</math> stehen. | ||
== | == | ||
Version vom 2. Juli 2010, 11:54 Uhr
- Eine Strecke
und eine Strecke 
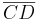stehen senkrecht aufeinander, wenn die Gerade 
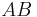und die Gerade 
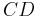senkrecht aufeinander stehen .
- Eine Strecke
- Eine Gerade
und eine Ebene 
stehen senkrecht aueinander, wenn es in einemindestens zwei Geraden gibt, die vollständig in liegen, und senkrecht auf stehen.
- Eine Gerade
- Nochmal richtig: Eine Gerade und eine Ebene stehen senkrecht aufeinander, wenn es in zwei sich schneidende Geraden gibt, die senkrecht auf stehen.
- Nochmal richtig: Eine Gerade
== Noch ein Versuch: ==
- Eine Strecke und eine Strecke 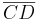stehen senkrecht aufeinander, wenn ein Punkt der Strecke jeweils den gleichen Abstand zu C und zu D hat oder umgekehrt.
- Eine Strecke
- Eine Gerade und eine Ebene stehen senkrecht aufeinander, wenn es in noch eine weitere Gerade gibt, die vollständig in liegt und senkrecht auf steht
- Eine Gerade
