Benutzer:Tutorin Anne: Unterschied zwischen den Versionen
(→Sommersemester 2014) |
|||
| Zeile 2: | Zeile 2: | ||
Weil ich mein Staatsexamen schon hinter mir habe, grüße ich euch dieses Semester aus Kamerun. Wasser, Strom und Internet fallen hier regelmäßig aus, so dass es passieren könnte, dass ich mal ein paar Tage nicht auf die Wikiseite komme. | Weil ich mein Staatsexamen schon hinter mir habe, grüße ich euch dieses Semester aus Kamerun. Wasser, Strom und Internet fallen hier regelmäßig aus, so dass es passieren könnte, dass ich mal ein paar Tage nicht auf die Wikiseite komme. | ||
--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 23:50, 5. Mai 2014 (CEST) | --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 23:50, 5. Mai 2014 (CEST) | ||
| + | Vom 13.06 bis 17.06 habe ich kein Internetzugang. Am 18.06. werde ich aber gerne alle eure Beiträge korregieren.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 09:11, 12. Jun. 2014 (CEST) | ||
==Newsticker== | ==Newsticker== | ||
<dpl> | <dpl> | ||
| Zeile 17: | Zeile 18: | ||
|} | |} | ||
| + | |||
= Mandala ganz einfach selbst gemacht!= | = Mandala ganz einfach selbst gemacht!= | ||
Version vom 12. Juni 2014, 08:11 Uhr
Sommersemester 2014
Weil ich mein Staatsexamen schon hinter mir habe, grüße ich euch dieses Semester aus Kamerun. Wasser, Strom und Internet fallen hier regelmäßig aus, so dass es passieren könnte, dass ich mal ein paar Tage nicht auf die Wikiseite komme. --Tutorin Anne (Diskussion) 23:50, 5. Mai 2014 (CEST) Vom 13.06 bis 17.06 habe ich kein Internetzugang. Am 18.06. werde ich aber gerne alle eure Beiträge korregieren.--Tutorin Anne (Diskussion) 09:11, 12. Jun. 2014 (CEST)
Newsticker
- Mikado (20.10.22, 19:38 -): Allgemeine Aspekte (23911 views)
- Mel123 (05.12.15, 16:51 -): Winkelmaß, Rechte Winkel, Orientierte Winkel WS 15 16 (1323 views)
- Mel123 (05.12.15, 16:41 -): Winkel, Innere eines Winkels, Nebenwinkel, Scheitelwinkel WS 15 16 (1740 views)
- Schnirch (28.05.15, 9:54 -): Winkelmaß, Rechte Winkel, Orientierte Winkel SoSe 15 (1188 views)
- Schnirch (28.05.15, 9:52 -): Winkel, Innere eines Winkels, Nebenwinkel, Scheitelwinkel SoSe 15 (1305 views)
- Schnirch (13.04.15, 9:08 -): Die WIKI-Seiten für die Primarstufe WS 14 15 (1362 views)
- EarlHickey (12.02.15, 16:07 -): Winkel, Innere eines Winkels, Nebenwinkel, Scheitelwinkel WS 14/15 (1997 views)
- EarlHickey (12.02.15, 14:08 -): Strecken und Halbgeraden WS 14/15 (2574 views)
- EarlHickey (09.02.15, 16:15 -): Lösung von Aufg. 5.1P (WS 14/15) (1594 views)
- EarlHickey (09.02.15, 14:43 -): Lösung von Zusatzaufgabe 4.3 P (WS 14/15) (929 views)
- EarlHickey (09.02.15, 12:26 -): Lösung von Aufgabe 4.3 P (WS 14/15) (1282 views)
- EarlHickey (09.02.15, 12:04 -): Lösung von Aufgabe 4.2 P (WS 14/15) (1509 views)
- EarlHickey (09.02.15, 0:20 -): Lösung von Zusatzaufgabe 3.3 P (WS 14/15) (1093 views)
- EarlHickey (08.02.15, 20:07 -): Lösung von Zusatzaufgabe 2.1P (WS 14 15) (1315 views)
- Schnirch (27.01.15, 13:59 -): Lösung von Zusatzaufgabe 13.1P (WS 14/15) (811 views)
- Schnirch (27.01.15, 13:58 -): Lösung von Aufgabe 13.4P (WS 14/15) (948 views)
- Schnirch (27.01.15, 13:57 -): Lösung von Aufgabe 13.3P (WS 14/15) (825 views)
- Schnirch (27.01.15, 13:57 -): Lösung von Aufgabe 13.2P (WS 14/15) (886 views)
- Schnirch (27.01.15, 13:56 -): Lösung von Aufgabe 13.1P (WS 14/15) (952 views)
- Schnirch (20.01.15, 13:01 -): Lösung von Zusatzaufgabe 12.1P (WS 14/15) (842 views)
- Schnirch (20.01.15, 12:08 -): Lösung von Aufgabe 12.4P (WS 14/15) (854 views)
- Schnirch (20.01.15, 12:07 -): Lösung von Aufgabe 12.3P (WS 14/15) (833 views)
- Schnirch (20.01.15, 12:07 -): Lösung von Aufgabe 12.2P (WS 14/15) (829 views)
- Schnirch (20.01.15, 12:06 -): Lösung von Aufgabe 12.1P (WS 14/15) (805 views)
- Schnirch (19.01.15, 13:17 -): Lösung von Aufgabe 11.3P (WS 14/15) (1182 views)
- Schnirch (19.01.15, 13:12 -): Lösung von Aufgabe 10.3P (WS 14/15) (1375 views)
- Schnirch (19.01.15, 13:07 -): Lösung von Aufg. 6.3P (WS 14/15) (1089 views)
- Schnirch (19.01.15, 13:00 -): Lösung von Aufg. 6.2P (WS 14/15) (1157 views)
- Schnirch (19.01.15, 12:56 -): Lösung von Aufg. 6.1P (WS 14/15) (965 views)
- Leuchtbärli (13.01.15, 21:06 -): Lösung von Aufgabe 11.1P (WS 14/15) (1145 views)
- Schnirch (13.01.15, 14:25 -): Lösung von Zusatzaufgabe 11.1P (WS 14/15) (789 views)
- Schnirch (13.01.15, 14:21 -): Lösung von Aufgabe 11.4P (WS 14/15) (997 views)
- Schnirch (13.01.15, 14:20 -): Lösung von Aufgabe 11.2P (WS 14/15) (903 views)
- Schnirch (07.01.15, 11:34 -): Lösung von Aufgabe 10.4P (WS 14/15) (844 views)
- Schnirch (07.01.15, 11:32 -): Lösung von Aufgabe 10.2P (WS 14/15) (819 views)
- Schnirch (07.01.15, 11:31 -): Lösung von Aufgabe 10.1P (WS 14/15) (960 views)
- Schnirch (16.12.14, 13:48 -): Lösung von Zusatzaufgabe 9.1 (WS 14/15) (790 views)
- Schnirch (16.12.14, 13:47 -): Lösung von Aufgabe 9.4P (WS 14/15) (877 views)
- Schnirch (16.12.14, 13:46 -): Lösung von Aufgabe 9.3P (WS 14/15) (941 views)
- Schnirch (16.12.14, 13:45 -): Lösung von Aufgabe 9.2P (WS 14/15) (947 views)
|}
Mandala ganz einfach selbst gemacht!
Wo sich überall Mathematik verbirgt?!
Die Idee kam so
Anleitung: Mein erster Beitrag im Wiki
Nach dem ihr euch mit einem Fantasienamen angemeldet habt, könnt ihr Beiträge einfügen. Dabei kann man zunächst etwas Reinschreiben und das geht so:
Die meisten Symbole sind ja selbsterklärend. Die Wichtigsten sind:
Nicht vergessen! Vor dem Speichern selbst das Layout mittels "Vorschau" überprüfen. Oft fehlen z.B. Zeilenumbrüche.
Am Rand findet ihr zur Orientierung die wichtigsten Dinge:
--Tutorin Anne 18:13, 16. Apr. 2013 (CEST)
Tabelle als Vorlage
| Voraussetzung | (V. hier eintragen) |
| Behauptung | (Beh. hier eintragen) |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | (Schritt 1 hier) | (Begründung 1) |
| 2 | (Schritt 2) | (Begründung 2) |
| 3 | (Schritt) | (Begründung) |
| 4 | (Schritt) | (Begründung) |
| Voraussetzung | ... |
| Behauptung | .... |
| Annahme | ... |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | ...) | ... |
| 2 | ... | ... |
| 3 | ... | ... |
| 4 | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
Beweis: Parallelentreue der Geradenspiegelung Z9.1 SS2013
| Voraussetzung | a II b, 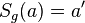 und und 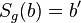
|
| Behauptung | a' II b' |
| Annahme | a' |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | 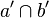 = {S'} = {S'} |
... |
| 2 | 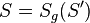 |
... |
| 3 | 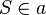 und und 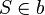 |
... |
| 4 | 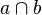 = {S} = {S} |
... |
| 5 | a' II b' | ... |
| 6 | Widerspruch zur Voraussetzung | ... |
WS12/13 Beweis zum Rechteck
Satz: Ein Rechteck hat 2 Symmetrieachsen.
| Voraussetzung | Rechteck 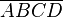
|
| Behauptung | 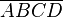 hat zwei Symmetrieachsen hat zwei Symmetrieachsen
|
Vorüberlegung: Es muss gezeicht werden, dass das Rechteck bei der Spiegelung an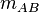 und
und 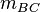 jeweils wieder auf sich abgebildet wird.
jeweils wieder auf sich abgebildet wird.
Beweisführung
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | m ist Mittelsenkrechte von  und n ist Mittelsenkrechte von und n ist Mittelsenkrechte von  |
Vor.; Def. Mittelsenkrechten |
| 2 | 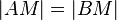 |
1.; Mittelsenkrechtenkriterium |
| 3 | 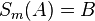 |
2.; Eigenschaften Geradenspiegelung (abstandserhaltend) |
| 4 | 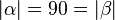 |
Vor. |
| 5 | 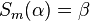 |
4. Eigenschaften Geradenspiegelung (Winkeltreue) |
| 6 | 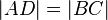 |
5. Vor. |
| 7 | 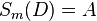 |
6. Eigenschaften Geradenspiegelung (abstandserhaltend) - müsste nicht Sm(D) = C sein? |
| 8 | 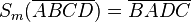 |
3.7. Eigenschaften Geradenspiegelung |
| 9 | m ist Symmetrieachse | 8. |
| 10 | n ist Symmetrieachse | analog Schritt 2-9 bezogen auf n |
Das ist jetzt mal so meine Idee, ich denke so könnte man es machen (mit richtiger Begründung!) - aber auch anders. Jetzt bitte Begründungen einfügen!!! --Tutorin Anne 18:58, 6. Feb. 2013 (CET)
SS12, Übung 10.3 Umkehrung des Basiswinkelsatzes, direkter Beweis
| Voraussetzung | Dreieck  mit üblicher Bezeichnung, mit üblicher Bezeichnung, 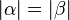
|
| Behauptung | 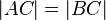
|
| Beweisschritt | Begründung |
|---|---|
1) m ist Mittelsenkrechte von  |
(Begründung 1) |
2) 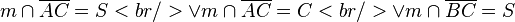 |
(Begründung 2) |
3) FAll 1)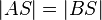 |
(Begründung) |
4) 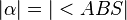 |
(Begründung) |
5) 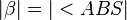 |
(Begründung) |
6) 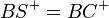 |
(Begründung) |
7) 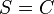 |
(Begründung) |
8) 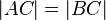 |
(Begründung) |
| 9) Fall 2) analog Fall 1 | - |
10) Fall 3) 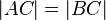 |
(Begründung) |
Funktionen (Elementare Funktionen SS 11)
Quadratische Funktion und ihr Graph, eine Parabel
Tutorium SS11
Tutorium 13, Aufgabe 1
| Voraussetzung | 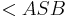 sei ein beliebiger Winkel sei ein beliebiger Winkel
|
| Behauptung | 1. Existenz einer Winkelhalbierenden 2. Eindeutigkeit dieser Wh |
Beweis zu 1.
z.z. Es exisitert ein Strahl 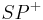 , für den gilt
, für den gilt 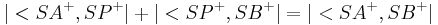 und
und 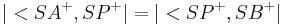 .
.
| 1) | 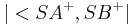 ist eine reele Zahl zwischen 0 und 180 ist eine reele Zahl zwischen 0 und 180 |
... |
| 2) | ... | ... |
| 3) | ... | ... |
| 4) | ... | ... |
| 5) | ... | ... |
Tutorium 3, Aufgabe 2