Auftrag der Woche 7 (WS 16 17): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 11: Zeile 11:
 
  Hallo AlanTu,<br/>
 
  Hallo AlanTu,<br/>
 
  das ist eine sehr schöne und klar verständliche GeoGebra-Applikation. Auch deine Anmerkungen sind richtig ;) <br/>
 
  das ist eine sehr schöne und klar verständliche GeoGebra-Applikation. Auch deine Anmerkungen sind richtig ;) <br/>
−
  Jetzt darf der Beobachter nur nicht auf Glasscheibe so schauen, dass die brennende Kerze <math>K_2</math> auf der Sichtlinie liegt (Stichwort kollinear und komplanar), sonst erkennt er den Trick. <br/>
+
  Jetzt darf der Beobachter nur nicht so auf Glasscheibe schauen, dass die brennende Kerze <math>K_2</math> auf der Sichtlinie liegt (Stichwort kollinear und komplanar), sonst erkennt er den Trick. <br/>
 
  Weiter so!<br/>
 
  Weiter so!<br/>
 
  Gruß --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 00:47, 18. Jan. 2017 (CET)
 
  Gruß --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 00:47, 18. Jan. 2017 (CET)

Version vom 18. Januar 2017, 00:53 Uhr

Zeigen Sie mit Hilfe einer GeoGebra-Applikation, dass beim Experiment mit der brennenden Kerze im Wasserglas die Position der gespiegelten Flamme unabhängig von der Position des Beobachters ist.

Lösung von AlanTu

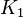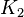Hier die Sicht von oben auf den Aufbau. K_1 ist die nicht brennende Kerze im Becherglas, B ist der Beobachter, K_2 ist die Position, an der man die brennende Kerze aufstellt.

Nun kann man B beliebig verschieben, wenn man genau auf 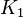K_1 blickt, landet die teilgespiegelte Sichtlinie immer genau auf 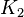K_2. Das passiert, da 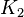K_2 genau der Punkt ist, den man erhält, wenn man 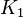K_1 an der Glasscheibe spiegelt. --AlanTu (Diskussion) 16:55, 17. Jan. 2017 (CET) 


Hallo AlanTu,

das ist eine sehr schöne und klar verständliche GeoGebra-Applikation. Auch deine Anmerkungen sind richtig ;) 

Jetzt darf der Beobachter nur nicht so auf Glasscheibe schauen, dass die brennende Kerze K_2 auf der Sichtlinie liegt (Stichwort kollinear und komplanar), sonst erkennt er den Trick. 

Weiter so!

Gruß --Tutor: Alex (Diskussion) 00:47, 18. Jan. 2017 (CET)
Aufgaben Wintersemester 2016/2017
Aufgaben Auftrag der Woche Quiz/Spiel der Woche Zusatzaufgaben
Woche 1 (17.10.–23.10.) Aufgaben 1 Auftrag der Woche 1 Quiz/Spiel der Woche 1 Zusatzaufgaben 1
Woche 2 (24.10.–30.10.) Aufgaben 2 Auftrag der Woche 2 Quiz/Spiel der Woche 2 Zusatzaufgaben 2
Woche 3 (31.10.–6.11.) Aufgaben 3 Auftrag der Woche 3 Quiz/Spiel der Woche 3 Zusatzaufgaben 3
Woche 4 (7.11.–13.10.) Aufgaben 4 Auftrag der Woche 4 Quiz/Spiel der Woche 4 Zusatzaufgaben 4
Woche 5 (14.11.–20.11.) Aufgaben 5 Auftrag der Woche 5 Quiz/Spiel der Woche 5 Zusatzaufgaben 5
Woche 6 (21.11.–27.11.) Aufgaben 6 Auftrag der Woche 6 Quiz/Spiel der Woche 6 Zusatzaufgaben 6
Woche 7 (28.11.–4.12.) Aufgaben 7 Auftrag der Woche 7 Quiz/Spiel der Woche 7 Zusatzaufgaben 7
Woche 8 (5.12.–11.12.) Probeklausur
Woche 9 (12.12.–18.12.) Aufgaben 9 Auftrag der Woche 9 Quiz/Spiel der Woche 9 Zusatzaufgaben 9
Xmas tree.svg Woche 10 (19.12.–25.12.) Aufgaben 10 Auftrag der Woche 10 Quiz/Spiel der Woche 10 Zusatzaufgaben 10
Woche 11 (9.1.–15.1.) Aufgaben 11 Auftrag der Woche 11 Quiz/Spiel der Woche 11 Zusatzaufgaben 11
Woche 12 (16.1.–22.1.) Aufgaben 12 Auftrag der Woche 12 Quiz/Spiel der Woche 12 Zusatzaufgaben 12
Von „http://geometrie.zum.de/index.php?title=Auftrag_der_Woche_7_(WS_16_17)&oldid=28999“