Lösung von Aufgabe 12.5: Unterschied zwischen den Versionen
(→Definition X.3: (entgegengesetzt liegende Winkel)) |
(→Lösung 1) |
||
| Zeile 10: | Zeile 10: | ||
::<math>BC'^+ \cong BC^+ \and B'C'^- \cong B'C^+</math>. | ::<math>BC'^+ \cong BC^+ \and B'C'^- \cong B'C^+</math>. | ||
<br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 22:24, 12. Jul. 2010 (UTC) | <br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 22:24, 12. Jul. 2010 (UTC) | ||
| − | + | <br /><br /> | |
| + | '''Lösung 2'''<br />Mir gefällt eigentlich dein zweiter Ansatz ganz gut. Allerdings verstehe ich nicht ganz, was du mit der Zwischenrelation gemeint hast. Ist das notwendig für die Definition? Mein Verbesserungsvorschlag wäre auch, so wenig Punkte wie möglich zu benutzen. Das würde dann ungefähr so aussehen:<br /><br />Zwei Winkel <math>\angle ABC</math> und <math>\angle A'CC'</math> heißen Stufenwinkel, wenn die Punkte <math>\ A</math> und <math>\ A'</math> bezüglich der Geraden <math>BC \ </math> in ein und derselben Halbebene liegen und <math> \operatorname{koll} \left( B, C, C' \right)</math> gilt.<br /><br />Was hältst du davon?<br />--[[Benutzer:Barbarossa|Barbarossa]] 20:29, 23. Jul. 2010 (UTC) | ||
==== Definition X.2: (Wechselwinkel) ==== | ==== Definition X.2: (Wechselwinkel) ==== | ||
Aktuelle Version vom 23. Juli 2010, 21:29 Uhr
Definieren Sie: Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel
Definitionen im Skript
Inhaltsverzeichnis |
Definition X.1: (Stufenwinkel)
Lösung 1
- Wenn zwei Geraden (
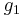 und
und 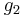 ) von einer dritten Geraden (
) von einer dritten Geraden (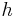 ) geschnitten werden,bezeichnet man die Winkel als Stufenwinkel, bei denen einer der begrenzenden Strahlen Teilmenge der selben Geraden (der Geraden
) geschnitten werden,bezeichnet man die Winkel als Stufenwinkel, bei denen einer der begrenzenden Strahlen Teilmenge der selben Geraden (der Geraden 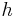 ) ist und bezüglich zu einem Punkt
) ist und bezüglich zu einem Punkt 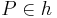 (der nicht zwischen
(der nicht zwischen 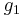 und
und 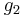 liegt) die selbe Richtung hat und deren jeweils anderer Strahl bezüglich der Geraden
liegt) die selbe Richtung hat und deren jeweils anderer Strahl bezüglich der Geraden 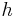 in der selben Halbebene liegen.
in der selben Halbebene liegen.
- Zwei Winkel
 und
und 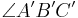 sind Stufenwinkel, wenn die Strahlen
sind Stufenwinkel, wenn die Strahlen 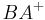 und
und 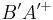 in der selben Halbebene bezüglich der Geraden
in der selben Halbebene bezüglich der Geraden 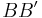 liegen und es gilt:
liegen und es gilt: 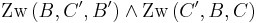 .
.
- Zwei Winkel
 und
und 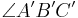 sind Stufenwinkel, wenn die Punkte
sind Stufenwinkel, wenn die Punkte  und
und 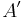 in der selben Halbebene bezüglich der Geraden
in der selben Halbebene bezüglich der Geraden 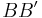 liegen und es gilt entweder:
liegen und es gilt entweder:
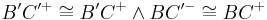 oder
oder
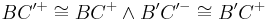 .
.
--Heinzvaneugen 22:24, 12. Jul. 2010 (UTC)
Lösung 2
Mir gefällt eigentlich dein zweiter Ansatz ganz gut. Allerdings verstehe ich nicht ganz, was du mit der Zwischenrelation gemeint hast. Ist das notwendig für die Definition? Mein Verbesserungsvorschlag wäre auch, so wenig Punkte wie möglich zu benutzen. Das würde dann ungefähr so aussehen:
Zwei Winkel  und
und 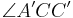 heißen Stufenwinkel, wenn die Punkte
heißen Stufenwinkel, wenn die Punkte  und
und 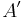 bezüglich der Geraden
bezüglich der Geraden 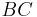 in ein und derselben Halbebene liegen und
in ein und derselben Halbebene liegen und 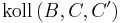 gilt.
gilt.
Was hältst du davon?
--Barbarossa 20:29, 23. Jul. 2010 (UTC)
Definition X.2: (Wechselwinkel)
Lösung 1
Zwei Winkel  und
und 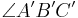 sind Wechselwinkel, wenn die Punkte
sind Wechselwinkel, wenn die Punkte  und
und 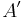 in verschiedenen Halbebenen bezüglich der Geraden
in verschiedenen Halbebenen bezüglich der Geraden 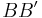 liegen und es gilt entweder:
liegen und es gilt entweder: 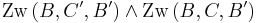 oder
oder 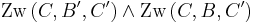
--Heinzvaneugen 22:24, 12. Jul. 2010 (UTC)
Definition X.3: (entgegengesetzt liegende Winkel)
Lösung 1
Zwei Winkel  und
und 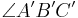 sind entgegengesetzt liegende Winkel (Nachbarwinkel), wenn die Punkte
sind entgegengesetzt liegende Winkel (Nachbarwinkel), wenn die Punkte  und
und 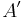 in der selben Halbebene bezüglich der Geraden
in der selben Halbebene bezüglich der Geraden 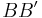 liegen und es gilt entweder:
liegen und es gilt entweder: 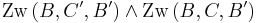 oder
oder 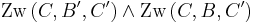
--Heinzvaneugen 22:24, 12. Jul. 2010 (UTC)
Lösung 2
Zwei WInkel 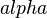 und
und 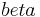 sind entgegengesetzt liegende Winkel, wenn
sind entgegengesetzt liegende Winkel, wenn 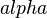 und
und 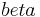 bezüglich der Geraden
bezüglich der Geraden  in ein und derselben Halbebene liegen, wobei gilt, dass jeweils ein Schenkel der Winkel eine Teilmenge dieser Geraden ist. Diese Schenkel haben entweder keinen Schnittpunkt gemeinsam oder der Schnitt der beiden Schenkel bildet eine Strecke.
in ein und derselben Halbebene liegen, wobei gilt, dass jeweils ein Schenkel der Winkel eine Teilmenge dieser Geraden ist. Diese Schenkel haben entweder keinen Schnittpunkt gemeinsam oder der Schnitt der beiden Schenkel bildet eine Strecke.
--Löwenzahn 09:32, 14. Jul. 2010 (UTC)

