Geradenspiegelungen: Unterschied zwischen den Versionen
(→Satz 2.1: (Abstandserhaltung von Geradenspiegelungen)) |
(→Satz 2.1: (Abstandserhaltung von Geradenspiegelungen)) |
||
| Zeile 128: | Zeile 128: | ||
| 5. | | 5. | ||
| <math> | \overline {BL}| = | \overline {B'L}|</math> | | <math> | \overline {BL}| = | \overline {B'L}|</math> | ||
| − | | <math>\ g</math> ist Mittelsenkrechte von <math>\overline{ | + | | <math>\ g</math> ist Mittelsenkrechte von <math>\overline{BB'}</math> |
|- | |- | ||
| 6. | | 6. | ||
| Zeile 144: | Zeile 144: | ||
Ergänzung: Für den Fall, das A und B nicht in der selben Halbebene bezüglich der Geraden s liegt, läuft der Beweis analog, nur dass die Winkel anderst benannt werden müssen. | Ergänzung: Für den Fall, das A und B nicht in der selben Halbebene bezüglich der Geraden s liegt, läuft der Beweis analog, nur dass die Winkel anderst benannt werden müssen. | ||
| − | Müsste es bei Fall 3 Schritt 5 nicht <math>\ g</math> ist Mittelsenkrechte von <math>\overline{BB'}</math> heißen oder bezieht man hier Fall 2 mit ein, sodass der Beweis formal und logisch richtig ist? --[[Benutzer:Andreas|Andreas]] 16:02, 30. Okt. 2010 (UTC) | + | Müsste es bei Fall 3 Schritt 5 nicht <math>\ g</math> ist Mittelsenkrechte von <math>\overline{BB'}</math> heißen oder bezieht man hier Fall 2 mit ein, sodass der Beweis formal und logisch richtig ist? Ja <math>\overline{BB'}</math> ist korrekt, habs geändert--[[Benutzer:Andreas|Andreas]] 16:02, 30. Okt. 2010 (UTC) |
Version vom 1. November 2010, 08:40 Uhr
Inhaltsverzeichnis |
Konstruktion des Bildes eines Punktes  bei einer Spiegelung an der Geraden
bei einer Spiegelung an der Geraden 
Übungsaufgabe
Es sei  ein Punkt der Ebene der nicht zur Geraden
ein Punkt der Ebene der nicht zur Geraden  dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von
dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von  bei der Spiegelung an
bei der Spiegelung an  . Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
. Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
| Nr. | Beschreibung des Schrittes | Begründung der Korrektheit des Schrittes |
|---|---|---|
| 1. | Wir fällen das Lot von  auf auf  . Den Schnittpunkt des Lotes mit der Geraden . Den Schnittpunkt des Lotes mit der Geraden  bezeichnen wir mit bezeichnen wir mit 
|
So bestimmen wir die kürzeste Strecke zwischen dem Punkt  und der Geraden und der Geraden  . Außerdem steht das Lot senkrecht auf . Außerdem steht das Lot senkrecht auf  , was die Voraussetzung dafür ist, dass , was die Voraussetzung dafür ist, dass  später Mittelsenkrechte werden kann. später Mittelsenkrechte werden kann.
|
| 2. | Nun tragen wir die Strecke 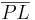 auf der Halbgeraden auf der Halbgeraden 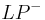 ab ab
|
Durch das Abtragen der Strecke bekommen wir auf beiden Seiten derHalbgeraden den gleichen Abstand vond er Geraden 
|
| 3. | Den entstandenen Punkt bezeichnen wir mit 
|
 ist der Bildpunkt von P bei der Geradenspiegelung an ist der Bildpunkt von P bei der Geradenspiegelung an  . Das wird dadurch ersichtlich, dass . Das wird dadurch ersichtlich, dass  und und  den gleichen Abstand zu den gleichen Abstand zu  haben und haben und  somit Mittelsenkrechte der Strecke somit Mittelsenkrechte der Strecke 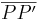 ist. ist.
|
Definition des Begriffs
Definition 2.1: (Spiegelung an der Geraden  )
)
- Es sei
 eine Gerade. Unter der Geradenspiegelung
eine Gerade. Unter der Geradenspiegelung 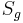 versteht man eine ....
versteht man eine ....
- Es sei
- Es sei
 eine Gerade und P ein Punkkt der Ebene. Unter der Geradenspiegelung
eine Gerade und P ein Punkkt der Ebene. Unter der Geradenspiegelung 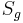 versteht man eine Abbildung der Ebene auf sich:
versteht man eine Abbildung der Ebene auf sich:
- Es sei
(1) Für den Fall dass P 
 : P = P'
: P = P'
(2) Für den fall dass P 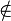
 : Die Gerade
: Die Gerade  ist Mittelsenkrechte der Strecke zwischen dem Punkt P und seinem Bildpunkt P'
ist Mittelsenkrechte der Strecke zwischen dem Punkt P und seinem Bildpunkt P'
Alternativ?
Es seien eine Gerade g und zwei Punkte A, A'  g. s ist genau dann Spiegelgerade des Punktes A, wenn gilt: s ist Mittelsenkrechte der Strecke AA'[Balken drüber].
g. s ist genau dann Spiegelgerade des Punktes A, wenn gilt: s ist Mittelsenkrechte der Strecke AA'[Balken drüber].
Die Geradenspiegelung als spezielle Bewegung
Satz 2.1: (Abstandserhaltung von Geradenspiegelungen)
- Jede Geradenspiegelung
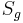 ist eine abstandserhaltende Abbildung.
ist eine abstandserhaltende Abbildung.
- Jede Geradenspiegelung
Beweis:
Es seien  ,
,  zwei Punkte, die an einer Geraden
zwei Punkte, die an einer Geraden  auf ihre Bilder
auf ihre Bilder 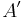 und
und 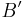 gespiegelt werden.
gespiegelt werden.
Wir unterscheiden drei Fälle:
1. 


Der Beweis ist trivial, da es sich bei dieser speziellen Geradenspiegelung um die Identität handelt.
2. 

 ,
, 
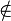

Den Schnittpunkt von 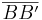 mit
mit  bezeichnen wir mit
bezeichnen wir mit 
| Nr. | Beschreibung des Schrittes | Begründung der Korrektheit des Schrittes |
|---|---|---|
| 1. |  = = 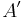
|
Definition Geradenspiegelung |
| 2. | 
|
 ist Mittelsenkrechte von ist Mittelsenkrechte von 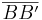
|
| 3. | 
|
Es handelt sich um dieselbe Gerade. |
| 4. | 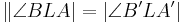 = 90° = 90°
|
 ist Mittelsenkrechte von ist Mittelsenkrechte von 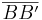
|
| 5. | 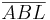 kongruent kongruent 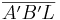
|
2. + 3. + 4. + SWS |
| 6. | 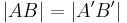
|
5. |
|}
3.
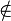

Den Schnittpunkt von 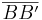 mit
mit  bezeichnen wir mit
bezeichnen wir mit 
Den Schnittpunkt von 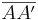 mit
mit  bezeichnen wir mit
bezeichnen wir mit 
| Nr. | Beschreibung des Schrittes | Begründung der Korrektheit des Schrittes |
|---|---|---|
| 1. | 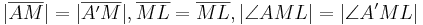 = 90° = 90°
|
 ist Mittelsenkrechte von ist Mittelsenkrechte von 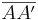
|
| 2. | 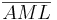 kongruent kongruent 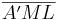
|
1. |
| 3. |  und und 
|
Wechselwinkelsatz, da 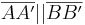
|
| 4. | 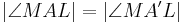 --> --> 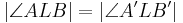
|
2. + 3. |
| 5. | 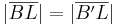
|
 ist Mittelsenkrechte von ist Mittelsenkrechte von 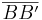
|
| 6. | 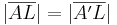
|
2. |
| 7. | 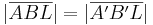
|
4. + 5. + 6. + SWS |
| 8. | 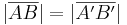
|
7. |
Ergänzung: Für den Fall, das A und B nicht in der selben Halbebene bezüglich der Geraden s liegt, läuft der Beweis analog, nur dass die Winkel anderst benannt werden müssen.
Müsste es bei Fall 3 Schritt 5 nicht  ist Mittelsenkrechte von
ist Mittelsenkrechte von 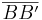 heißen oder bezieht man hier Fall 2 mit ein, sodass der Beweis formal und logisch richtig ist? Ja
heißen oder bezieht man hier Fall 2 mit ein, sodass der Beweis formal und logisch richtig ist? Ja 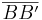 ist korrekt, habs geändert--Andreas 16:02, 30. Okt. 2010 (UTC)
ist korrekt, habs geändert--Andreas 16:02, 30. Okt. 2010 (UTC)