Drehungen 2010: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition verstanden?)
(→‎Konstruktionsbeschreibung)
Zeile 7: Zeile 7:
 
Das Bild von <math>\ P</math> bei einer Drehung um <math>\ Z</math> wird wie folgt konstruiert:
 
Das Bild von <math>\ P</math> bei einer Drehung um <math>\ Z</math> wird wie folgt konstruiert:
  
−
Fall 1: <math>\ P \equiv  Z</math>
+
Fall 1: <math>\ P \equiv  Z</math> dann <math> \ P \equiv \P'</math>
  
 
... .
 
... .
Zeile 33: Zeile 33:
 
| ...
 
| ...
 
|}
 
|}
 +
 
== Definition des Begriffs der Drehung um einen Punkt <math>\ Z</math> mit dem Drehwinkel <math>\ \alpha</math> ==
 
== Definition des Begriffs der Drehung um einen Punkt <math>\ Z</math> mit dem Drehwinkel <math>\ \alpha</math> ==
 
==== Definition 5.1: (Drehung um einen Punkt <math>\ Z</math> mit dem Drehwinkel <math>\ \alpha</math>====
 
==== Definition 5.1: (Drehung um einen Punkt <math>\ Z</math> mit dem Drehwinkel <math>\ \alpha</math>====

Version vom 11. November 2010, 11:49 Uhr

Inhaltsverzeichnis

Konstruktion des Bildes eines Punktes P bei einer Drehung um Z mit dem Drehwinkel \alpha

Konstruktionsbeschreibung

Es seien \ Z und \ P zwei Punkte der Ebene. Ferner sei \ \alpha ein gerichteter Winkel.

Das Bild von \ P bei einer Drehung um \ Z wird wie folgt konstruiert:

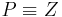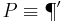
Fall 1: \ P \equiv Z dann \ P \equiv \P'

... .

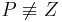
Fall 2: \ P \not\equiv Z


Konstruktion des Bildes eines Punktes \ P bei einer Drehung um \ Z mit dem Drehwinkel \ \alpha im Falle \ P \not\equiv Z
Schrittnr. Konstruktionsschritt Begründung der Korrektheit des Konstruktionsschrittes
(I) ... ...
(II) ... ...
(III) ... ...

Definition des Begriffs der Drehung um einen Punkt \ Z mit dem Drehwinkel \ \alpha

Definition 5.1: (Drehung um einen Punkt \ Z mit dem Drehwinkel \ \alpha

Es sei \ Z ein Punkt der Ebene und \ \alpha ein gerichteter Winkel. Unter der Drehung um \ Z mit dem Drehwinkel \ \alpha versteht man eine Abbildung der Ebene auf sich für die folgendes gilt:
  1. ...
  2. ...

Definition verstanden?




1. Welche der folgenden Aussagen sind wahr?

(a) Der Punkt \ A wird bei der Drehung um \ Z mit dem Drehwinkel \ \alpha = 45^\circ auf den Punkt \ B abgebildet.
(b) Es gibt eine Drehung für die gleichzeitig gilt: Das Bild von \ B ist \ E, das Bild von \ E ist \ H, das Bild von \ H ist \ K, ..., das Bild von \ W ist \ B_1
(c) (b) ist äquivalent zu: Es gibt einen Kreis auf dem die Punkte \ B, E, H, K, U, Q, R, W, B_1 liegen.
(d) Der Punkt \ A wird bei der Drehung um \ Z mit dem Drehwinkel \ \alpha = 40^\circ auf den Punkt \ D abgebildet.
(e) Die Winkelhalbierenden der Winkel bei der obigen Darstellung, deren Scheitelpunkte alle auf ein und demselben Kreis liegen, sind parallel zueinander.

Punkte: 0 / 0
Von „http://geometrie.zum.de/index.php?title=Drehungen_2010&oldid=4748“