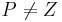Drehungen 2010
Konstruktion des Bildes eines Punktes  bei einer Drehung um
bei einer Drehung um  mit dem Drehwinkel
mit dem Drehwinkel 
Konstruktionsbeschreibung
Es seien  und
und  zwei Punkte der Ebene. Ferner sei
zwei Punkte der Ebene. Ferner sei  ein gerichteter Winkel.
ein gerichteter Winkel.
Das Bild von  bei einer Drehung um
bei einer Drehung um  wird wie folgt konstruiert:
wird wie folgt konstruiert:
Fall 1: 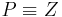 ,dann ist
,dann ist  (P' ist das Bild)
(P' ist das Bild)
Fall 2: 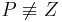 , dann
, dann
| Schrittnr. | Konstruktionsschritt | Begründung der Korrektheit des Konstruktionsschrittes |
|---|---|---|
| (I) | Konstruiere den Strahl 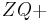 an den Strahl an den Strahl 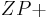 mit dem Winkel mit dem Winkel  so an, dass die positive Orientierung von so an, dass die positive Orientierung von  für < für < 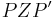 erhalten bleibt. erhalten bleibt.
|
Winkelkonstruktionsaxiom |
| (II) | Trage die Strecke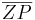 auf auf 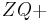 an an  ab und nenne den Punkt ab und nenne den Punkt  . .
|
Axiom vom Lineal--Tja??? 10:56, 11. Nov. 2010 (UTC) |
Konstruktionsbeschreibung für Konstruktion nur mit Zirkel und Lineal
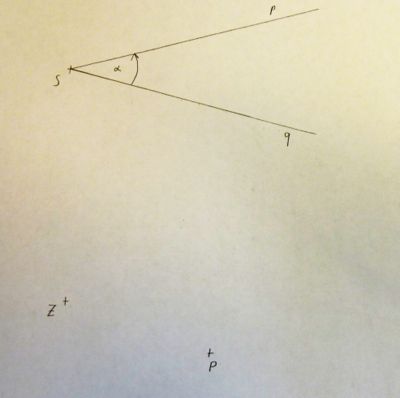
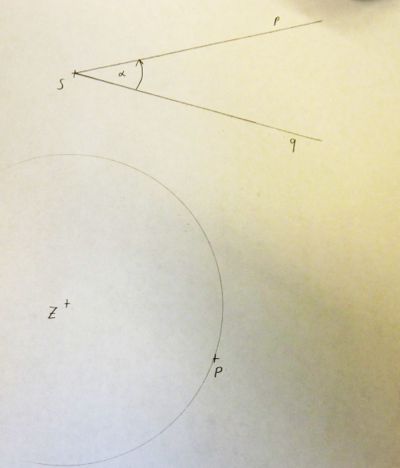
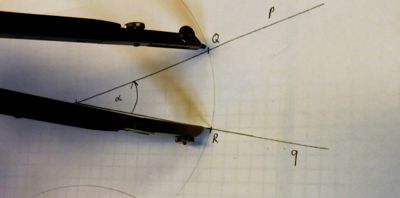
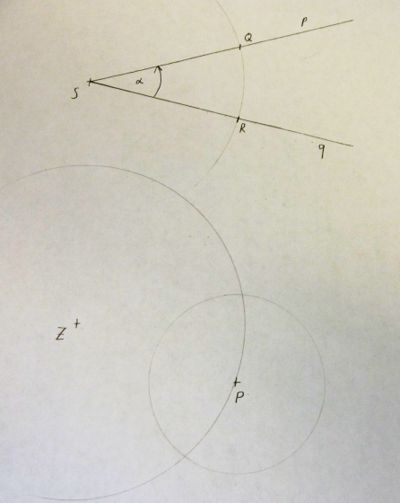
1) Wir zeichnen mit dem Zirkel einen Kreis k1 um Z, der durch P geht.
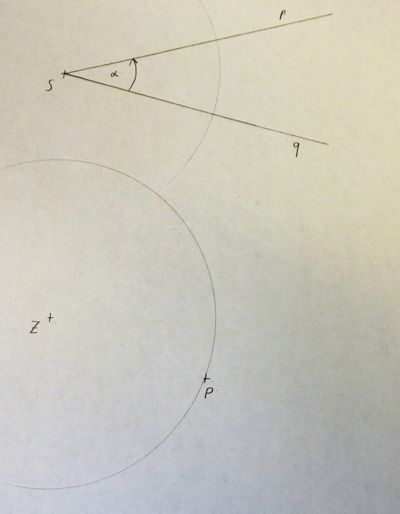
2) Mit demselben Radius zeichnen wir nun einen Kreis um S.
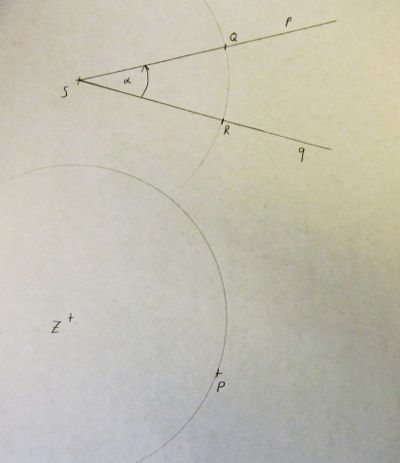
3) Die Schnittpunkte mit den Schenkeln p un q bezeichnen wir mit R und Q.
4) Wir nimm die Strecke RQ in die Zirkelspanne,
5) zeichne mit der Strecke RQ als Radius einen zweiten Kreis k2 um P.
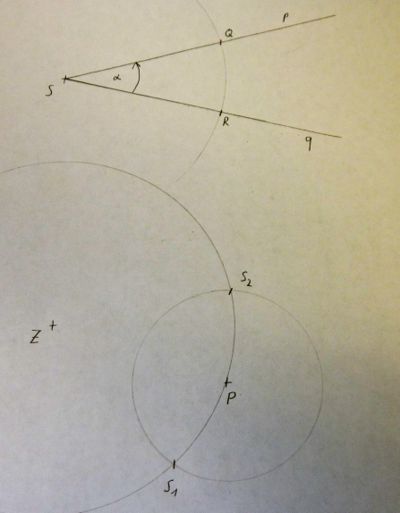
6) Die Schnittpunkte der beiden Kreise k1 und k2 benennen wir mit S1 und S2.
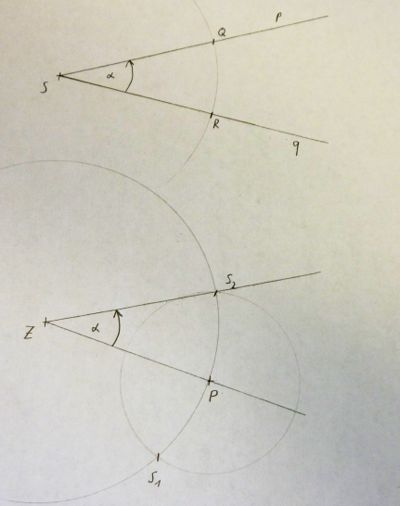
7) Da der Winkel α mathematisch positiv gerichtet ist, muss auch der Drehwinkel der Abbildung positiv gerichtet sein.
8) Wir zeichnen die Strahlen ZP+ und ZS2+.
9) S2 ist P', der Bildpunkt von P.
--Nicola 12:35, 11. Nov. 2010 (UTC)
--Andreas 13:00, 11. Nov. 2010 (UTC)
--phhd_mat 12:35, 11. Nov. 2010 (UTC)
Konstruktionsbeschreibung 2:
1. Zeichne einen Kreis k1 mit Radius 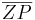 um den Mittelpunkt Z.
um den Mittelpunkt Z.
2. Zeichne einen Kreis mit Radius 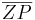 um den Mittelpunkt S (Scheitelpunkt des Winkels
um den Mittelpunkt S (Scheitelpunkt des Winkels  ). Nenne die Schnittpunkte R und Q.
). Nenne die Schnittpunkte R und Q.
3. Zeichne einen Kreis k2 mit Radius 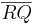 um den Mittelpunkt P.
um den Mittelpunkt P.
4. Die Kreise k1 und k2 haben zwei Schnittpunkte. Nenne sie P1' und P2'. Zeichne die Strahlen ZP1'+, ZP+ und ZP2'+. Je nach Drehrichtung des Winkels  , ist P1' bzw. P2' der Bildpunkt von P.
, ist P1' bzw. P2' der Bildpunkt von P.
--morita 11:13, 15. Nov. 2010 (UTC)
Definition des Begriffs der Drehung um einen Punkt  mit dem Drehwinkel
mit dem Drehwinkel 
Definition 5.1: (Drehung um einen Punkt  mit dem Drehwinkel
mit dem Drehwinkel 
- Es sei
 ein Punkt der Ebene und
ein Punkt der Ebene und  ein gerichteter Winkel. Unter der Drehung um
ein gerichteter Winkel. Unter der Drehung um  mit dem Drehwinkel
mit dem Drehwinkel  versteht man eine Abbildung der Ebene auf sich für die folgendes gilt:
versteht man eine Abbildung der Ebene auf sich für die folgendes gilt:
- Es sei
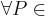 der Ebene gilt:
der Ebene gilt:
Definition verstanden?
2 Sätze und der dazugehörige Beweis
Ich habe mal zwei Beweise angefertigt und stelle sie an dieser Stelle allen zur Verfügung um darüber zu diskutieren. Gibt es Fehler in der Logik, der Schreibweise oder bei den Begründungen? Ich bin mir eben nicht ganz sicher :)
Satz: Jede Drehung 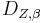 ist eine Bewegung.
ist eine Bewegung.
Beweis
Voraussetzung: Drehung D um Punkt Z mit dem Winkel 
Behauptung: |PQ|=|P'Q'|
| Beweisschritt | Begründung |
|---|---|
1) 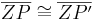
|
folgt unmittelbar aus der Definition: (Drehung) |
2) 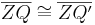
|
folgt unmittelbar aus der Definition: (Drehung) |
3) 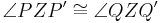
|
folgt unmittelbar aus der Definition: (Drehung) |
4) 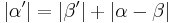
|
rechnen in den reellen Zahlen, folgt aus Schritt 3, da 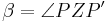 und und 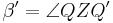
|
5) 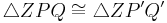
|
folgt aus den Schritten 1-4, sws |
6) 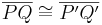
|
folgt aus Schritt 5 |
7) 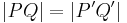
|
folgt aus Schritt 6, q.e.d |
--Andreas 14:22, 9. Nov. 2010 (UTC)
Satz: Wenn eine Bewegung  genau einen Fixpunkt Z hat, dann ist
genau einen Fixpunkt Z hat, dann ist  eine Drehung um den Fixpunkt Z.
eine Drehung um den Fixpunkt Z.
Beweis
Voraussetzung:  ist eine Bewegung,
ist eine Bewegung,  hat genau eine Fixpunkt Z
hat genau eine Fixpunkt Z
Behauptung: 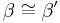
| Beweisschritt | Begründung |
|---|---|
1. 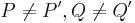
|
folgt unmittelbar aus der Voraussetzung (genau ein Fixpunkt Z) |
2. 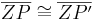
|
folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend) |
3. 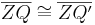
|
folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend) |
4. 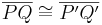
|
folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend) |
5. 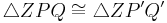
|
sss, folgt aus den Schritten 2-4 |
6. 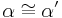 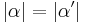
|
folgt aus Schritt 5 |
7.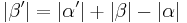  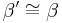
|
rechnen in den reellen Zahlen, Schritt 6 |
--Andreas 15:13, 11. Nov. 2010 (UTC)
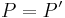 , falls
, falls 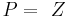
 und |
und |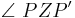 | =
| = 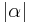 , falls
, falls