Lösung von Aufg. 13.2 (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Satz VI. 1 \frac{1}{2})
Zeile 6: Zeile 6:
 
:: Es sei <math>\ SW^+</math> die Winkelhalbierende des Winkels <math>\angle ASB</math>. Dann gilt <math>| \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |</math>.
 
:: Es sei <math>\ SW^+</math> die Winkelhalbierende des Winkels <math>\angle ASB</math>. Dann gilt <math>| \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |</math>.
  
−
Hab ihn gefunden :) --[[Benutzer:Andreas|Tutor Andreas]] 10:52, 8. Jul. 2011 (CEST)
+
Hab ihn gefunden :) --[[Benutzer:Andreas|Tutor Andreas]] 10:52, 8. Jul. 2011 (CEST) <br /><br />
 +
 
 +
Das steckt ja schon in der Semantik des Wortes Winkelhalbierende drin - das beweisen wir nicht, das sollten wir einfach mal glauben :-)
 +
<br /><br />
 +
Nein Quatsch. Die Frage ist hier jedoch, von welcher Definition wir ausgehen. Wenn wir von der Definition ausgehen, dass "die Winkelhalbierende SW^+ ein Strahl im Inneren eines Winkels <math>\angle ASB</math> ist. Dieser STrahl teilt die WInkel folgendermaßen auf: <math>| \angle ASW | = | \angle WSB |</math>", dann haben wir tatsächlich leichtes Spiel, da wegen dem Winkeladditionsaxiom zwei Teilwinkel die Größe des ursprünglichen Winkels ergeben. Somit ist <math>| \angle ASW | + | \angle WSB | = | \angle ASB |</math>". Wegen <math>| \angle ASW | = | \angle WSB |</math>" gilt nach Rechnen in R dass
  
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]

Version vom 8. Juli 2011, 22:32 Uhr

Beweisen Sie Satz VI.eineinhalb

Wo steht dieser Satz ? --Peterpummel 12:31, 7. Jul. 2011 (CEST)

Satz VI.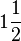 1 \frac{1}{2}
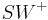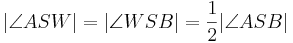Es sei \ SW^+ die Winkelhalbierende des Winkels \angle ASB. Dann gilt | \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |.

Hab ihn gefunden :) --Tutor Andreas 10:52, 8. Jul. 2011 (CEST)

Das steckt ja schon in der Semantik des Wortes Winkelhalbierende drin - das beweisen wir nicht, das sollten wir einfach mal glauben :-)

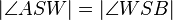Nein Quatsch. Die Frage ist hier jedoch, von welcher Definition wir ausgehen. Wenn wir von der Definition ausgehen, dass "die Winkelhalbierende SW^+ ein Strahl im Inneren eines Winkels \angle ASB ist. Dieser STrahl teilt die WInkel folgendermaßen auf: | \angle ASW | = | \angle WSB |", dann haben wir tatsächlich leichtes Spiel, da wegen dem Winkeladditionsaxiom zwei Teilwinkel die Größe des ursprünglichen Winkels ergeben. Somit ist 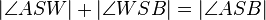| \angle ASW | + | \angle WSB | = | \angle ASB |". Wegen 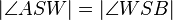| \angle ASW | = | \angle WSB |" gilt nach Rechnen in R dass

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._13.2_(SoSe_11)&oldid=8079“