Lösung von Aufg. 15.2 (SoSe 11): Unterschied zwischen den Versionen
| Zeile 13: | Zeile 13: | ||
c) Beweisen Sie den Satz aus b) indirekt.<br /><br /> | c) Beweisen Sie den Satz aus b) indirekt.<br /><br /> | ||
| + | |||
| + | [[Datei:Muffinkopf_Übung_15_Nr.2.jpg]]--[[Benutzer:Muffinkopf|Muffinkopf]] 18:28, 24. Jul. 2011 (CEST) | ||
Version vom 24. Juli 2011, 17:28 Uhr
Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.
a) Welche Bedingung ergibt sich für den dargestellten Winkel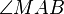 
, wenn die Gerade g zur Tangente am Kreis k im Punkt A wird?
b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ...
Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ist der Winkel <MAB ein rechter Winkel. M ist dabei der Mittelpunkt von k und Bϵg--...s... 19:47, 23. Jul. 2011 (CEST)
Müsste man nicht sagen, dann steht die Streccke AM senkrecht auf g?
Hab mein Problem mit 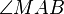weil, wenn g Tangente an k ist dann ist A ja eigentlich gleich B und der Winkel ist so nicht zu verwenden, oder täusche ich mich da? Benutzer:kopfnicker 23:16, 23. Jul. 2011
Du kannst den Winkel ja auch mit dem Punkt Z benennen, wenn du die Gerade g mit BZ bezeichnest. Oder ist dein Problem ein anderes? --Tutor Andreas 11:00, 24. Jul. 2011 (CEST)
Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ist die Strecke vom Kreismittelpunkt M zum Berührpunkt A das Lot --Muffinkopf 18:02, 24. Jul. 2011 (CEST)
c) Beweisen Sie den Satz aus b) indirekt.
--Muffinkopf 18:28, 24. Jul. 2011 (CEST)
d) Gilt auch die Umkehrung des Satzes aus b)?
