Lösung von Aufg. 15.2 (SoSe 11)

Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.
a) Welche Bedingung ergibt sich für den dargestellten Winkel 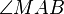$\angle MAB$, wenn die Gerade g zur Tangente am Kreis k im Punkt A wird?

b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ...

Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ist der Winkel <MAB ein rechter Winkel. M ist dabei der Mittelpunkt von k und Bϵg--...s... 19:47, 23. Jul. 2011 (CEST)

Müsste man nicht sagen, dann steht die Streccke AM senkrecht auf g? Hab mein Problem mit 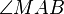$\angle MAB$ weil, wenn g Tangente an k ist dann ist A ja eigentlich gleich B und der Winkel ist so nicht zu verwenden, oder täusche ich mich da? Benutzer:kopfnicker 23:16, 23. Jul. 2011
Du kannst den Winkel ja auch mit dem Punkt Z benennen, wenn du die Gerade g mit BZ bezeichnest. Oder ist dein Problem ein anderes? --Tutor Andreas 11:00, 24. Jul. 2011 (CEST)

Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ist die Strecke vom Kreismittelpunkt M zum Berührpunkt A das Lot --Muffinkopf 18:02, 24. Jul. 2011 (CEST)

c) Beweisen Sie den Satz aus b) indirekt.

--Muffinkopf 18:28, 24. Jul. 2011 (CEST) Hast du vielleicht eie Skizze dazu? --Verteidigungswolf 20:28, 24. Jul. 2011 (CEST)

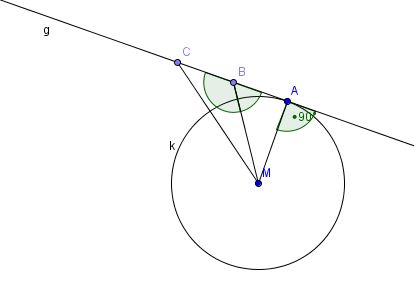hier die Skizze dazu --Muffinkopf 07:37, 25. Jul. 2011 (CEST)

Danke erstmal für die Skizze! Nur irgendwie versteh ich nicht genau, wo du die Annahme verwendest...--Verteidigungswolf 11:57, 25. Jul. 2011 (CEST)

@Muffinkopf: Bei deinem ersten Schritt schneidest du einen Punkt mit einer Gerade, aber das geht doch gar nicht. Oder verstehe ich den Schritt falsch.--Teufelchen 17:08, 26. Jul. 2011 (CEST)

Ich hab's mal mit fast der gleichen Beweisidee, aber einer viel schlechteren Skizze versucht:



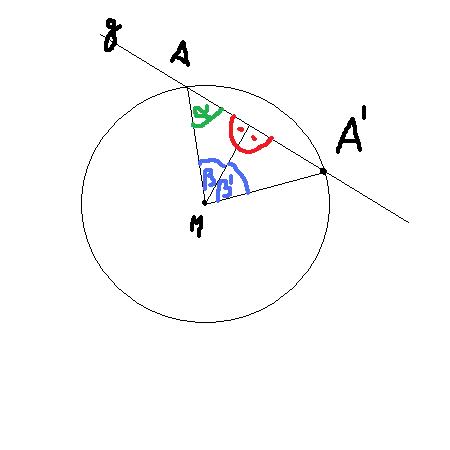
Meine Voraussetzung ist, dass g mit dem Kreis genau einen Punkt, nämlich A, gemeinsam hat.
Meine Annahme (für den indirekten Beweis) lautet, dass g nicht senkrecht auf MA steht, sondern unter dem Winkel $\alpha$ schneidet. Dabei entscheide ich mich dafür, dass $\alpha$ der (immer vorhandene) kleinere der beiden Schnittwinkel ist (nach Rechnen in R und Supplememtaxiom).
1. Jetzt fälle ich das Lot von M auf g (Begründung: Existenz und Eindeutigkeit des Lotes).
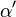2. Jetzt messe ich $\alpha$ (Winkelmaßaxiom) und trage einen gleich großen Winkel $\alpha'$ auf der anderen Halbebene bzgl des Lotes an. (Winkelkonstruktionsaxiom)
3. Jetzt messe ich die Strecke A-Fußpunkt (Abstandsaxiom) und trage den Abstand auf dem Strahl Fußpunkt-A^- ab (Axiom vom Lineal). Den neuen Endpunkt der neuen Strecke nenne ich A'.
4. Jetzt betrachte ich das Dreieck A-M-Fußpunkt und das Dreieck Fußpunkt-M-A' und stelle fest, sie haben einen rechten Winkel am Fußpunkt, die Strecke Fußpunkt-M und den Winkel $\beta$ bzw. den kongruent konstruierten Winkel 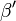$\beta'$ gemeinsam, sind also nach WSW-Satz kongruent.
5. Da die Seite A'M aber damit genauso lang ist wie die Seite AM, welche wiederum der Kreisradius war (aus Tangentendefinition), muss Punkt A' auch zum Kreis gehören, denn das ist die Menge aller Punkte (der Ebene), die zu M diesen Abstand haben.
6. Da A' aber auch auf der Geraden g liegt (über Supplementaxiom am Fußpunkt), hat g in A' einen zweiten gemeinsamen Punkt mit dem Kreis, was der Voraussetzung widerspricht.
Ist das so (abgesehen von den nicht formal korrekten Bezeichnungen der Seiten - LaTex ist etwas kompliziert) korrekt oder habe ich was übersehen? --WikiNutzer 12:57, 27. Jul. 2011 (CEST)

d) Gilt auch die Umkehrung des Satzes aus b)?