Lösung von Aufgabe 3.3 (WS 11/12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 70: Zeile 70:
  
 
Somit muss die Halbgerade l die Winkelschneidende sein.--[[Benutzer:RicRic|RicRic]]
 
Somit muss die Halbgerade l die Winkelschneidende sein.--[[Benutzer:RicRic|RicRic]]
 +
== Noch ein Versuch ==
 +
 +
{| class="wikitable"
 +
|-
 +
| Beweisschritt || Begründung
 +
|-
 +
| (1) Dreieck SQM ist rechtwinklig || Satz des Tales
 +
|-
 +
| (2) Dreieck SMP ist rechtwinklig || Satz des Tales
 +
|-
 +
| (3) <math>\overline{SP} = \overline{SQ}</math>  und  <math>\overline{PM} = \overline{MQ}</math> || Konstruktionsvorschrift
 +
|-
 +
| (4) sin(<math>\angle p,l</math>) =  <math>\overline{MQ}</math> : <math>\overline{SP}</math>|| Trigonometrie , (1)
 +
|-
 +
| (5) sin(<math>\angle q,l</math>) =  <math>\overline{PM}</math> : <math>\overline{SP}</math>|| Trigonometrie , (2)
 +
|-
 +
| (6) sin(<math>\angle q,l</math>) =  <math>\overline{PM}</math> : <math>\overline{SP}</math> = <math>\overline{MQ}</math> : <math>\overline{SP}</math>|| (3) und (5)
 +
|-
 +
| (7) sin(<math>\angle q,l</math>) =  sin(<math>\angle p,l</math>) || (6) und (4)
 +
|-
 +
| (8) <math>\angle q,l</math> =  <math>\angle p,l</math> || (7)
 +
|}
 +
--[[Benutzer:Flobold|Flobold]] 14:21, 1. Nov. 2011 (CET)

Version vom 1. November 2011, 14:21 Uhr

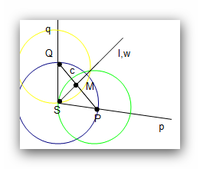
Wir gehen von folgender Definition aus:
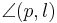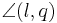Eine Winkelhalbierende eines Winkels \angle (p,q) ist ein Strahl l, der im Inneren des Winkels \angle (p,q) liegt, den Scheitel des Winkels \angle (p,q) als Anfangspunkt besitzt und diesen Winkel in zwei gleich große Winkel \angle (p,l) und \angle (l,q) unterteilt.
Außerdem sei folgende genetische Definition gegeben:

  • Gegeben sei ein Winkel \angle (p,q).
  • Man konstruiere auf den beiden Schenkeln des Winkels \angle (p,q) zwei Punkte P und Q, die vom Scheitel S des Winkels \angle (p,q) gleich weit entfernt sind.
  • Man konstruiere die Strecke \overline{PQ}.
  • Man konstruiere den Mittelpunkt M der Strecke \overline{PQ}.
  • Man konstruiere den Strahl w mit dem Anfangspunkt S, der durch den Punkt M verläuft.
  • Dieser Strahl w ist die Winkelhalbierende.

Beweisen Sie, dass durch diese Konstruktionsvorschrift tatsächlich die Winkelhalbierende entsprechend der angegebenen Definition entsteht.


  • Wenn man die Konstruktionsvorschrift befolgt und eine Winkelhalbierende erhält, ist die Konstruktionsvorschrift dann bewiesen?

--Todah raba 18:06, 28. Okt. 2011 (CEST)

Beweisschritt Begründung
(1) 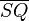\overline{SP} = \overline{SQ} Voraussetzung
(2) 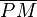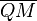\overline{PM} = \overline{QM} Konstruktionsvorschrift
(3) 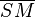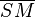\overline{SM} = \overline{SM} Konstruktionsvorschrift
(4) 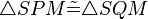\triangle {SPM} \tilde = \triangle {SQM} SSS,(1),(2),(3)
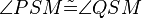(5) \angle {PSM} \tilde = \angle {QSM} (4)

--Mathenerds 10:40, 29. Okt. 2011 (CEST)


weiterer Lösungsversuch

  • An dieser Stelle bitte ich den Autor einige Dinge näher zu erläutern, um eventuelle Missverständnisse zu vermeiden. --Tutor Andreas 14:40, 31. Okt. 2011 (CET)

Winkelhalb.png

Voraussetzungen:

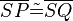
\overline{SP} \tilde {=} \overline{SQ}

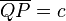\overline{QP} =c Was bedeutet c bzw c1 oder c2? Sind hier reelle Zahlen gemeint? --Tutor Andreas 14:40, 31. Okt. 2011 (CET)

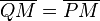
\overline{QM} = \overline{PM}

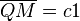
\overline{QM} =c1

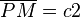
\overline{PM} =c2

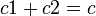
c1 + c2 = c

Behauptung:

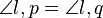
\angle l,p = \angle l,q

Beweis:

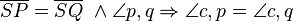\overline{SP} = \overline{SQ}\ \wedge \angle p,q \Rightarrow \angle c,p = \angle c,q SWS Dreiecksatz berachtes Dreick: S,P,Q

Was soll hier gemeint sein? --Tutor Andreas 14:40, 31. Okt. 2011 (CET)
* Ich betrachte hier das Dreieck S,P,Q und stelle fest, dass die Srecken S,Q und S,P der Voraussetzung nach gleich lang sind,
ebenfalls ist der Winkel q,p gegeben, daraus folgere ich, dass der Winkel c,p und der Winkel c,q konguent sein müssen. 
Da wenn bei einem Dreieck zwei aneinanderliegende Seiten und der dazwischenligende Winkel geben ist, 
die restlichen Winkel und die weitere Seite auch feststehen. Bei dem Sonderfall, dass die zwei Seiten,
wie hier auch noch gleich lang sind müssen die Winkel auch konguent sein.

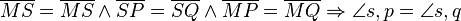\overline{MS} = \overline{MS} \wedge \overline{SP} = \overline{SQ} \wedge \overline{MP} = \overline{MQ} \Rightarrow \angle s,p = \angle s,q SSS Dreiecksatz betrachtete Dreicke S,M,P und S,Q,P

Somit muss die Halbgerade l die Winkelschneidende sein.--RicRic

Noch ein Versuch

Beweisschritt Begründung
(1) Dreieck SQM ist rechtwinklig Satz des Tales
(2) Dreieck SMP ist rechtwinklig Satz des Tales
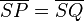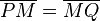(3) \overline{SP} = \overline{SQ} und \overline{PM} = \overline{MQ} Konstruktionsvorschrift
(4) sin(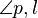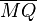\angle p,l) = \overline{MQ} : \overline{SP} Trigonometrie , (1)
(5) sin(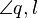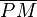\angle q,l) = \overline{PM} : \overline{SP} Trigonometrie , (2)
(6) sin(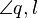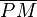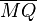\angle q,l) = \overline{PM} : \overline{SP} = \overline{MQ} : \overline{SP} (3) und (5)
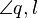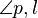(7) sin(\angle q,l) = sin(\angle p,l) (6) und (4)
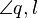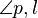(8) \angle q,l = \angle p,l (7)

--Flobold 14:21, 1. Nov. 2011 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_3.3_(WS_11/12)&oldid=9114“