Lösung von Aufg. 8.1 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \pi \left|…“) |
RicRic (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \pi \left| AB \right|</math> und <math>\overline{AB} \subset \overline{AB^{*}}</math>. | Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \pi \left| AB \right|</math> und <math>\overline{AB} \subset \overline{AB^{*}}</math>. | ||
| + | |||
| + | <br /> | ||
| + | Vor.: Es sei <math>\overline{AB}</math> eine Strecke.<br /><br /> | ||
| + | Beh.: <math>\exists ! \overline{AB*} | \left| AB* \right|= \pi \left| AB \right| \wedge \overline{AB} c \overline{AB*}</math> <br /><br /> | ||
| + | Bew.:Existenz: | ||
| + | |||
| + | {| class="wikitable sortable" | ||
| + | !Schritt!!Begründung | ||
| + | |- | ||
| + | | (2) <math>\exists \ AB^{+} : A,B\in \ AB^{+}</math> || Def Strahl | ||
| + | |- | ||
| + | | (3) <math>\exists B* : \left| AB* \right| = \pi \left| AB \right| \wedge B* \in \ AB^{+}</math> || A vom Lineal, (2) | ||
| + | |- | ||
| + | | (4) <math>\left| AB* \right| > \left| AB \right|</math> || (3),da Abstand <math> \pi </math> mal so groß | ||
| + | |- | ||
| + | | (5) <math>\left| AB \right| + \left| BB* \right| = \left| AB* \right|</math> || zw. Relation, (4),(3) | ||
| + | |- | ||
| + | | (6) zw(A,B,B*) || (5) | ||
| + | |- | ||
| + | | <math>\overline{AB} c\overline{AB*}</math> || (6),(2),(3) | ||
| + | |} | ||
| + | <br /><br /> | ||
| + | Bew.:Eindeutigkeit:<br /> | ||
| + | Ann.: <math>\left(\exists \overline{AB*} | \left| AB* \right|= \pi \left| AB \right| \wedge \overline{AB} c \overline{AB*}\right) \wedge \left( \exists \overline{AC*} | \left| AC* \right|= \pi \left| AB \right| \wedge \overline{AB} c \overline{AC*}\right)\wedge B*\neq C*</math><br /> | ||
| + | |||
| + | {| class="wikitable sortable" | ||
| + | !Schritt!!Begründung | ||
| + | |- | ||
| + | | (1) <math>\exists \ AB^{+} : A,B\in \ AB^{+}</math> || Def Strahl | ||
| + | |- | ||
| + | | (2) <math>\exists B* : \left| AB* \right| = \pi \left| AB \right| \wedge B* \in \ AB^{+}</math> || A vom Lineal, (1) | ||
| + | |- | ||
| + | | (3) <math>\exists C* : \left| AC* \right| = \pi \left| AB \right| \wedge C* \in \ AB^{+}</math> || A vom Lineal, (1) | ||
| + | |- | ||
| + | | (4) <math>\left| AB* \right| = \pi \left| AB \right| \wedge \left| AC* \right| = \pi \left| AB \right|</math> || (2),(3) | ||
| + | |- | ||
| + | | (5) <math>\left| AB* \right| = \left| AC* \right|</math>|| Rechen in R, (4) | ||
| + | |- | ||
| + | | (6) <math> B*\in \ AB^{+} \wedge C*\in \ AB^{+}</math> || (2),(3) | ||
| + | |- | ||
| + | | (7)<math>B* = C* \lightning</math>zur Ann. ,diese ist zu Verwerfen|| A vom Lineal (6),(4)--[[Benutzer:RicRic|RicRic]] 13:32, 4. Dez. 2011 (CET) | ||
| + | |} | ||
| + | |||
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
Version vom 4. Dezember 2011, 13:32 Uhr
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  mit
mit  und
und  .
.
Vor.: Es sei  eine Strecke.
eine Strecke.
Beh.: 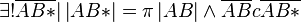
Bew.:Existenz:
| Schritt | Begründung |
|---|---|
(2) 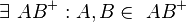 |
Def Strahl |
(3) 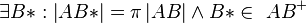 |
A vom Lineal, (2) |
(4) 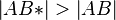 |
(3),da Abstand 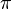 mal so groß mal so groß
|
(5) 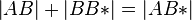 |
zw. Relation, (4),(3) |
| (6) zw(A,B,B*) | (5) |
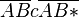 |
(6),(2),(3) |
Bew.:Eindeutigkeit:
Ann.: 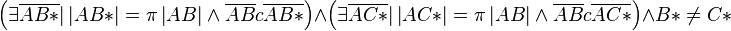
| Schritt | Begründung |
|---|---|
(1) 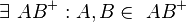 |
Def Strahl |
(2) 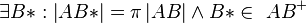 |
A vom Lineal, (1) |
(3) 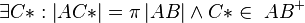 |
A vom Lineal, (1) |
(4) 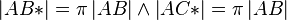 |
(2),(3) |
(5) 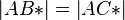 |
Rechen in R, (4) |
(6) 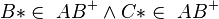 |
(2),(3) |
| (7)Fehler beim Parsen(Unbekannte Funktion „\lightning“): B* = C* \lightning zur Ann. ,diese ist zu Verwerfen | A vom Lineal (6),(4)--RicRic 13:32, 4. Dez. 2011 (CET) |

