12)

Definieren Sie den Begriff Strahl $\ AB^{+}$. Verwenden Sie dabei den Begriff Strecke.

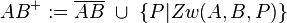$\ AB^{+} := \overline{AB} \ \cup \ \{P| Zw (A, B, P)\}$ --Todah raba 16:29, 7. Dez. 2011 (CET)

Falsch: $AB^{+} := \overline{AB} \ \cup \ \{\overline{BP}|  Zw (A, B, P)\}$--RicRic 21:50, 8. Dez. 2011 (CET)

Veränderte Version nach Übung am Di --RicRic 18:10, 14. Dez. 2011 (CET)

Eine dieser beiden Lösungsvorschläge stimmt nicht - aber welcher und warum nicht? --Spannagel 12:38, 10. Dez. 2011 (CET)

Bei der Definition von RicRic werden zwei Strecken vereinigt, die beide endlich sind. Das müsste falsch sein, da der Strahl $AB^+$ in eine Richtung unendlich ist. Wäre es auch möglich die Definition in einem Satz zu schreiben ? Mathenerds 12:27, 11. Dez. 2011 (CET)
Ja Strecken sind schon endlich, aber meine Überlegung ist, dass bei der zweiten Strecke P eine Varialbe ist die irgendwo nach $\overline{AB}$ sich befindet, also auch in der Unendlichkeit.--RicRic 16:16, 11. Dez. 2011 (CET)

- Es seien A und B zwei verschiedene Punkte und g die Gerade durch A und B. $AB^+$ ist die Vereinigung von $\overline {AB}$ und alle Punkte P für die gilt: P ist Element von g und P ist nicht Element von $\overline {AB}$. --Schmarn 10:49, 14. Dez. 2011 (CET)
@Schmarn, nee das ist "Schmarn":-), denn wenn du die Gerade nimmst und dann die Strecke AB davon und mit allen Punken vereinigst, welche noch auf der Geraden liegen und nicht auf der Strecke AB, so erhälst du wieder die Gerade und nicht die Halbgrade(oder du meinst mit AB die Grade, dann erhäst du nur die Strecke und keinen Strahl.--RicRic 18:00, 14. Dez. 2011 (CET)