12)

Aufgabe 14.1

Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt.

Lösung von Aufg. 14.1 WS_11/12

Aufgabe 14.2

Beweisen Sie die Existenz und Eindeutigkeit des Umkreises eines Dreiecks.

Lösung von Aufg. 14.2 WS_11/12

Aufgabe 14.3

Beweisen Sie: Die Winkelhalbierenden eines Dreiecks schneiden sich in genau einem Punkt.

Lösung von Aufg. 14.3 WS_11/12

Aufgabe 14.4

Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.
a) Welche Bedingung ergibt sich für den dargestellten Winkel 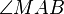$\angle MAB$, wenn die Gerade g zur Tangente am Kreis k im Punkt A wird?

b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ...

c) Beweisen Sie den Satz aus b) indirekt.

d) Gilt auch die Umkehrung des Satzes aus b)? Beweisen Sie dies.

e) Entwickeln Sie ein Tangentenkriterium aus b) und d)

Lösung von Aufg. 14.4 (WS_11/12

Aufgabe 14.5

Beweisen Sie die Existenz und Eindeutigkeit des Inkreises eines Dreiecks.

Lösung von Aufg. 14.5 WS_11/12