Serie 5 (WS 12 13)
Aus Geometrie-Wiki
Version vom 22. November 2012, 13:53 Uhr von *m.g.* (Diskussion | Beiträge)
Inhaltsverzeichnis |
Aufgaben zum Abstand
Aufgabe 5.1
Satz:
- Es seien
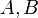 und
und  drei paarweise verschiedene Punkte. Wenn der Punkt
drei paarweise verschiedene Punkte. Wenn der Punkt  zwischen den Punkten
zwischen den Punkten  und
und  liegt, dann liegt weder
liegt, dann liegt weder  zwischen
zwischen  und
und  noch
noch  zwischen
zwischen  und
und  .
.
- Es seien
Beweisen Sie diesen Satz.
Lösung von Aufgabe 5.1_S (WS_12_13)
Aufgabe 5.2
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:





Lösung von Aufgabe 5.2_S (WS_12_13)
Aufgabe 5.3
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:
Wenn 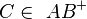 und
und 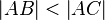 dann gilt
dann gilt 
Lösung von Aufgabe 5.3_S (WS_12_13)
Aufgabe 5.4
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  auf
auf  mit
mit 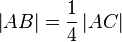 und
und 


Lösung von Aufgabe 5.4_S (WS_12_13)
Weitere Aufgabe zur Inzidenz
Aufgabe 5.5
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).
Lösung von Aufg. 5.5_S (WS_12_13)

