12)
Aus Geometrie-Wiki
Version vom 24. Januar 2012, 01:36 Uhr von Adores (Diskussion | Beiträge)
Beweisen Sie: Wenn  ein Punkt außerhalb der Geraden
ein Punkt außerhalb der Geraden  ist, dann gibt es eine Gerade
ist, dann gibt es eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Kann man, um diese Implikation zu beweisen, das Parallelnaxiom verwenden?
- Mann kann es in der absoluten Geometrie beweisen. D.h. ohne Parallelaxiom. --RicRic 07:53, 23. Jan. 2012 (CET
Vor: P, g, P 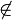 g
g
Beh: P  h
h 
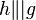
| Beweisschritt | Begründung |
|---|---|
1)  R, L : R,L R, L : R,L  g g
|
Axiom I.2 |
2)  l: P, L l: P, L  l l  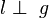  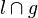 = {L} = {L}
|
Ex. und Eind. Lot, (1) |
3)  Q: Q Q: Q  gP+ gP+  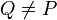
|
Definition Halbebene |
4)  PA+: PA+: 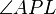 = 90 = 90  PA+ Teilmenge von lQ+ PA+ Teilmenge von lQ+
|
Axiom IV.2, (2), (3) |
5) 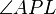 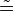 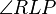
|
(2), (4) |
6) 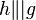
|
(5), Umkehrung Wechselwinkelsatz |
| q.e.d. |
--Adores 01:36, 24. Jan. 2012 (CET)

