Lösung von Aufgabe 9.4P (SoSe 13)

m sei Mittelsenkrechte der Strecke $\overline{AB}$. Beweisen Sie durch Kontraposition: $\left| AP \right| =\left| BP \right|\Rightarrow P\in m$
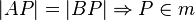
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.

Kontraposition lautet: P 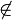$\not\in$ m$\Rightarrow$ IAPI$\neq$ IBPI Wenn P nicht Element m ist, dann sind 2 Fälle zu betrachten. Weil P kann einmal in der Halbebene von m liegen in der B liegt oder P kann in der Halbebene von m liegen in der A liegt.

IAPI=IBPI, m ist Mittelsenkrechte der Strecke AB|
Behauptung	(P ist Element m)

Annahme: P ist nicht Element m

Betrachtung: Punkt P liegt in der selben Halbebene von m wie B

Nr.	Beweisschritt	Begründung
1	(Strecke BP geschnitten mit m=leere Menge )	(Def. HE, Annahme)
2	(Strecke AP geschnitten mit m =(R))	(1,)
3	(R ist Element Strecke AP)	(2)
4	(Zw(ARP))	(Def. ZW, 3)

(5) IARI + IRPI= IAPI 4

(6) IStreckeAPI > IStrecke BPI 5

WIEDERSPRUCH ZUR VORAUSSETZUNG. ANNAHME VERWERFEN, BEHAUPTUNG STIMMT.
--Blumenkind 17:49, 4. Jul. 2013 (CEST)BLUMENKIND 17:47, 4.JULI