Definitionen in der Mathematik SoSe 11
Erkenntnisse aus dem einführenden Beispiel
Wir haben im einführenden Beispiel festgestellt, dass Eratosthenes zur Umfangsbestimmung der Erde z. B. den Wechselwinkelsatz benutzte. Um einen mathematischen Satz verstehen oder auch beweisen zu können müssen die Begriffe und ihre Bedeutung exakt bestimmt, d. h. definiert werden.
Um einen Begriff definieren zu können braucht man weitere Begriffe, mit denen man den neu zu definierten Begriff um- bzw. beschreibt. Auch diese weiteren Begriffe müssen aber im Vorfeld natürlich festgelegt, also auch definiert werden. Dies lässt sich dann endlos so weiterführen und man käme aus der Endlosschleife des Begriffedefinierens nicht heraus.
Deshalb hat man in der Mathematik möglichst wenige grundlegende Begriffe, so genannte Grundbegriffe eingeführt, die nicht weiter bestimmt werden müssen (in der Geometrie z. B. die Begriffe: Punkte, Geraden, Ebenen, Abstand ...).
Man legt nur, mit Hilfe der so genannten Axiome, die Beziehungen zwischen den Grundbegriffen fest.
Was ist eine Definition?
- Eine Definition ist in der Mathematik eine Begriffsbestimmung, die nur aus Grundbegriffen oder bereits definierten Begriffen besteht.
- Eine Definition ist nicht beweisbar und damit auch nicht wahr oder falsch sondern höchstens sinnvoll oder nicht sinnvoll.
Anmerkung: Sie können z. B. eine Raute auf verschiedene Arten definieren. Alle Definitionen sollten aber immer die uns bekannte Raute beschreiben und nicht plötzlich eine andere Figur (Fünfeck, Trapez etc.). Das wäre dann natürlich schon falsch! Beispiele für in diesem Sinne falsche Definitionen finden Sie in den Übungen 1. - Eine Definition sollte so wenig wie möglich und so viel wie nötig beinhalten.
Anmerkung: Dabei schwingt immer eine gewisse Unschärfe mit, die sich didaktisch begründen lässt:
Bsp. Definition Rechteck:
Ein Rechteck ist ein Viereck mit drei rechten Innenwinkel.
Diese Definition ist so knapp wie möglich gehalten. Insbesondere genügt es die Eigenschaft: "besitzt drei rechte Innenwinkel" zu beschreiben, da sich der vierte rechte Innenwinkel zwangsläufig ergibt. In der Regel wird man hier aber ein Rechteck als Viereck mit vier rechten Innenwinkel definieren, da diese Definition insbesondere für Schülerinnen und Schüler einsichtiger und griffiger ist.
Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulieren
Es gibt verschiedene Arten, Definitionen zu formulieren.
Beispiel 1: ggT zweier ganzer Zahlen
Die Begriffe Teiler und Euklidischer Algorithmus seien im Folgenden bereits exakt definiert.
Das Übliche, die Realdefinition
- Es seien
 und
und  zwei ganze Zahlen.
zwei ganze Zahlen. 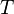 sei die Menge aller Zahlen, die sowohl Teiler von
sei die Menge aller Zahlen, die sowohl Teiler von  als auch von
als auch von  sind. Die größte Zahl der Menge
sind. Die größte Zahl der Menge 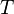 heißt größter gemeinsamer Teiler der Zahlen
heißt größter gemeinsamer Teiler der Zahlen  und
und  .
.
- Es seien
Konventionaldefinition, das Ganze in "wenn-dann"
- Wenn eine Zahl
 sowohl die ganze Zahl
sowohl die ganze Zahl  als auch die ganze Zahl
als auch die ganze Zahl  teilt und es keine Zahl
teilt und es keine Zahl  gibt, die auch
gibt, die auch  und
und  teilt und dabei größer als
teilt und dabei größer als  ist, dann ist
ist, dann ist  der größte gemeinsame Teiler von
der größte gemeinsame Teiler von  und
und  .
.
- Wenn eine Zahl
Schön, aber wie bekomme ich den ggT: die genetisch, operative Definition
- Der letzte von 0 verschiedene Rest, den man bei Anwendung des Euklidischen Algorithmus auf die ganzen Zahlen
 und
und  erhält, ist der größte gemeinsame Teiler der Zahlen
erhält, ist der größte gemeinsame Teiler der Zahlen  und
und  .
.
- Der letzte von 0 verschiedene Rest, den man bei Anwendung des Euklidischen Algorithmus auf die ganzen Zahlen
Beispiel 2: Drachenviereck
Die Begriffe Dreieck, Viereck, Diagonale, Eckpunkt, Geradenspiegelung und achsensymmetrisch seien im Folgenden bereits definiert.
Realdefinition
- Ein Viereck, bei dem die eine Diagonale Teilmenge der Mittelsenkrechten seiner anderen Diagonale ist, heißt Drachenviereck.
Konventionaldefinition
- Wenn ein Viereck achsensymmetrisch bezüglich einer Geraden ist, die durch zwei Eckpunkte des Vierecks geht, dann heißt das Viereck Drachenviereck.
genetisch, operative Definition
- Es sei
 ein Dreieck und
ein Dreieck und 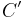 das Bild von
das Bild von  bei der Spiegelung an
bei der Spiegelung an  . Das Viereck
. Das Viereck 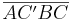 ist ein Drachenviereck.
ist ein Drachenviereck.
- Es sei
Ein wenig Didaktik: Definitionen auf verschiedenen Niveaustufen
Aus didaktischer Sicht lassen sich Definitionen auf verschiedenen Niveaustufen formulieren.
Das nachfolgende Skript gibt weitere Informationen:
* Definitionen
Entwicklung einer "neuen" Definition
Im Folgenden wollen wir versuchen, den (ihnen vermutlich wenig geläufigen) Begriff Ellipse zu definieren. Konstruktiv lässt sich eine Ellipse mit Hilfe der sogenannten Gärtnerkonstruktion, wie im folgenden Video, erzeugen.
Bemerkung zu obigem Video: Das geht natürlich noch schöner. Ansporn für Sie?
In einer ersten intuitiven Definition können wir also sagen:
- Eine Ellipse ist eine Figur mit zwei Brennpunkten
- Eine Ellipse ist ein gestauchter Kreis
- Eine Ellipse ist ein gestreckter Kreis
- Eine Ellipse ist das, was bei der Gärtnerkonstruktion entsteht. (Vorlesung 11.4.11
--Schnirch 15:39, 11. Apr. 2011 (CEST)
Das folgende Applet empfindet die Gärtnerkonstruktion nach.
Aufgaben:
- Experimentieren Sie nun mit dem Applet und machen Sie sich dabei die mathematischen Zusammenhänge klar (Tipp: Bewegen Sie den Punkt P und beobachten Sie die Strecken a und b).
Welche Zusammenhänge entdecken Sie?
- Versuchen Sie nun aus den Erkenntnissen eine formale Definition des Begriffs
Ellipse zu entwickeln.
- Können Sie nun den Begriff Kreis unter Verwendung des Oberbegriffs Ellipse definieren?
Vereinbarung: Wir setzen ebene Geometrie voraus.
Definition E.1: Ellipse
- Es seien
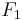 und
und 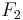 zwei Punkte. Unter der Ellipse mit den Brennpunkten
zwei Punkte. Unter der Ellipse mit den Brennpunkten 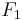 und
und 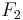 versteht man die Menge aller Punkte
versteht man die Menge aller Punkte  für die gilt, dass die Summe der Abstände
für die gilt, dass die Summe der Abstände 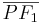 und
und 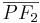 konstant ist. (Vorlesung: 11.04.11) --Schnirch 16:03, 11. Apr. 2011 (CEST)
konstant ist. (Vorlesung: 11.04.11) --Schnirch 16:03, 11. Apr. 2011 (CEST)
- Es seien
Frage: Brennpunkt ist kein Grundbegriff und ein bislang nicht definierter Begriff, muss er aus diesem Grund nicht auch noch definiert werden? --mm_l 20:09, 17. Apr. 2011 (CEST)}}
Definition K.1: Kreis als spezielle Ellipse
- Ein Kreis ist eine Ellipse, deren Brennpunkte
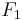 und
und 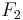 identisch sind.--MMaike 13:54, 13. Apr. 2011 (CEST)
identisch sind.--MMaike 13:54, 13. Apr. 2011 (CEST)
- Ein Kreis ist eine Ellipse, deren Brennpunkte
Zurückführen auf bereits vorhanden Definitionen: Verwenden von Oberbegriffen
Das Haus der Vierecke
[ www.ph-heidelberg.de is not an authorized iframe site ]
Obige Flash-Applikation wurde von Frau Andrea Spitz im Rahmen des Seminars "Erstellen von Multimediaanwendungen für den Unterricht" generiert.
Übungsaufgabe 1.3 der ersten Serie
Im Folgenden seien die Begriffe n-Eck, Seite eines n-ecks, Ecke eines n-Ecks bereits definiert. Ergänzen Sie die folgenden Definitionen. Beziehen Sie sich dabei jeweils auf den nächst höheren Oberbegriff.
Definition: Viereck
- Ein Viereck ist ein n-Eck mit n=4--*Osterhase* 13:22, 12. Apr. 2011 (CEST)
Definition: Trapez
- Ein Trapez ist ein Viereck mit zwei gegenüberliegenden parallelen Seiten. --Eiermanns 14:04, 12. Apr. 2011 (CEST)
Ein Trapez ist ein Viereck mit einem Paar paralleler Seiten. --Flo 21 22:54, 13. Apr. 2011 (CEST)
Definition: Parallelogramm
Ein Parallelogramm ist ein Viereck mit zwei Paar paralleler Seiten.--Flo 21 00:41, 13. Apr. 2011 (CEST)
Definition: gleichschenkliges Trapez
- Wenn bei einem Trapez die beiden nicht parallelen Seiten ein und denselben Abstand zwischen den Parallelen hat, dann ist es ein gleichschenkliges. --Flo 21 00:48, 13. Apr. 2011 (CEST)
Diese Definition erscheint mir noch etwas unklar. Was versteht man in diesem Fall unter "Abstand" (sollte genauer erklärt werden). Vielleicht gibt es noch andere Definitionen, die eindeutig ist.--Tutor Andreas 09:19, 13. Apr. 2011 (CEST)
- Ist ein Trapez, bei welchem die Diagonalen gleich lang sind.--Eng.MODs 10:15, 13. Apr. 2011 (CEST)
Gute Idee! --Tutorin Anne 13:01, 15. Apr. 2011 (CEST)
- Ein Trapez,bei dem die nicht parallelen Seiten gleich lang sind, heißt gleichschenkliges Trapez.--SeanJohn 15:59, 13. Apr. 2011 (CEST)
Eine weiter Möglichkeit, die noch nicht ganz korrekt ist. Kann man das für ALLE gleichs.Tra. sagen?--Tutorin Anne 13:01, 15. Apr. 2011 (CEST)
- wie sieht es denn aus mit: "Wenn die senkrechte Mittellinie der beiden parallelen Seiten eines Trapezes identisch sind und zugleich Symmetrieachse des Trapezes, dann ist das Trapez ein gleichschenkliches Trapez."? --HecklF 22:48, 14. Apr. 2011 (CEST)
Gute Idee, aber 1. Was ist eine Mittellinie? 2. Wie viel Informationen für diese Definition sind wirklich nötig?--Tutorin Anne 13:01, 15. Apr. 2011 (CEST)
Ein Trapez mit einem rechten Winkel, welches an diesem gespiegelt ist, ist ein gleichschenkliges Trapez.--Gueldaglart 15:42, 15. Apr. 2011 (CEST)
Was bedeutet "an einem Winkel spiegeln"? Wie ist ein Winkel definiert und ist die Definition dadurch sinnvoll? --Tutor Andreas 09:43, 17. Apr. 2011 (CEST)
Ein gleichschenkliges Trapez ist ein Viereck mit zwei zueinander parallelen Seiten, wobei diese eine gemeinsame Mittelsenkrechte haben.--Geometriker 12:43, 21. Apr. 2011 (CEST)
Definition: Rechteck
Ein Viereck mit vier rechten Innenwinkel heißt Rechteck. --Flo 21 00:45, 13. Apr. 2011 (CEST)
Eine Definition sollte immer so viel Information wie nötig, aber so wenig wie möglich enthalten. Geht es denn auch anders? Tipp: Über Parallelogramme definieren. --Tutor Andreas 09:23, 13. Apr. 2011 (CEST)
statt 4 rechten Innenwinkeln nur 3 verwenden. --Flo 21 22:52, 13. Apr. 2011 (CEST)
Ein Rechteck ist ein Parallelogramm mit einem rechten Winkel.
Wenn noch kein Parallelogramm def. ist: Ein 4 Eck bei welchem die Diagonale gleich lang sind und sich halbieren.--Eng.MODs 10:07, 13. Apr. 2011 (CEST)
Definition: Quadrat
Ein Viereck mit vier gleich langen Seiten und einem rechten Winkel heißt Quadrat.
--Flo 21 00:43, 13. Apr. 2011 (CEST)
steht schon gut da !
Wenn ein Viereck vier gleich lange Seiten hat und einen rechten Winkel besitzt, dann ist es ein Quadrat.--SeanJohn 15:53, 13. Apr. 2011 (CEST)
Definition: Drachen
Wenn zwei SteckenDiagonalen senkrecht aufeinander stehen und eine Strecke die andere halbiert, dann ist es ein Drachen. --Flo 21 00:44, 13. Apr. 2011 (CEST)Die Änderung in "Diagonalen" müsste die Def. "richtig" werden lassen, oder?--Flo 21 22:49, 13. Apr. 2011 (CEST)
Ein 4 Eck, bei welchem die Diagonalen senkrecht aufeinander stehen eine Diagonale wird halbiert halbieren.--Eng.MODs 10:10, 13. Apr. 2011 (CEST)
Halbieren sich die Diagonalen bei einem Drachen gegenseitig oder wird hier eine bestimmte "Art der Drachen" beschrieben? --Tutor Andreas 19:15, 14. Apr. 2011 (CEST)
Sind das Drachen, bzw. ist die zweite Konstruktion eine Raute? --Tutor Andreas 09:31, 13. Apr. 2011 (CEST)
Ein Viereck, bei dem eine Diagonale die Mittelsenkrechte der anderen Diagonale ist, heißt Drachen.--SeanJohn 15:50, 13. Apr. 2011 (CEST)
ist ein Viereck, bei dem eine Diagonale Symetrieachse ist --Gueldaglart 18:32, 13. Apr. 2011 (CEST)
Ein Drache ist ein Viereck mit senkrecht aufeinander stehenden Diagonalen.--Geometriker 12:49, 21. Apr. 2011 (CEST)
Ist diese Definition hinreichend, um Drachenvierecke wie wir sie kennen zu definieren?--Tutorin Anne 21:27, 25. Apr. 2011 (CEST)
Definition: Raute
Wenn zwei Diagonalen senkrecht aufeinander stehen und sie sich gegenseitig halbieren, dann ist das Viereck eine Raute. --Flo 21 00:44, 13. Apr. 2011 (CEST)
Ein Viereck, bei dem jede Diagonale die Mittelsenkrechte der anderen ist, heißt Raute.--SeanJohn 15:46, 13. Apr. 2011 (CEST)
Eine Raute ist ein Viereck mit vier gleich langen Seiten.--Flo 21 22:51, 13. Apr. 2011 (CEST)
Es kann nur eine geben - oder?
[ www.ph-heidelberg.de is not an authorized iframe site ]
Das obige Video wurde von Prof. Dr. Filler erstellt.
Definition E.2: Ellipse
- Es sei
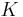 ein Doppelkegel und
ein Doppelkegel und  eine Ebene. Wenn
eine Ebene. Wenn  den Doppelkegel
den Doppelkegel 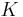 derart schneidet, dass die Spitze der Doppelkegel
derart schneidet, dass die Spitze der Doppelkegel 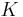 nicht Element der Ebene
nicht Element der Ebene  ist, dann heißt
ist, dann heißt  Ellipse. --MMaike 14:01, 13. Apr. 2011 (CEST)
Ellipse. --MMaike 14:01, 13. Apr. 2011 (CEST)
- Es sei
--*m.g.* 13:04, 18. Apr. 2011 (CEST):
Dass die Spitze des Kegels nicht zur Ebene gehört, ist notwendig dafür, dass beim Schnitt eine Ellipse entsteht, hinreichend allerdings nicht:
Falls die Ebene den Doppelkegel allerdings waagrecht schneidet entsteht ein Kreis.--Geometriker 13:00, 21. Apr. 2011 (CEST)
| Parabel | Hyperbel |
 |

|
Übungsaufgabe 1.5 der Serie 1
- Definition E.1 und Definition E.2 sind zwei verschiedene Definitionen ein und desselben Begriffs. Geht das? Diskutieren Sie!
....
Darf es ein wenig mehr sein? Ellipse als Hypozykloide
Mit einem Spirograph (Spielzeug)12px lassen sich geometrische Kurven zeichnen. Läßt man dabei ein kleineres Zahnrad innerhalb eines großen Zahnrades abrollen entstehen sogenannte Hypozykloiden. Ellipsen sind besondere Hypozykloiden. Die folgende Flash-Applikation wurde im Seminar "Erstellen von Multimedianwendungen für den Unterricht" im Sommersemester 2008 erstellt. Versuchen Sie mit der Applikation eine Ellipse zu generieren (Was aussieht wie ein Ellipse ist dann auch eine). Definieren Sie dann den Begriff Ellipse als spezielle Hypozykloide.
[ www.ph-heidelberg.de is not an authorized iframe site ]
Die Kurve wird durch Klicken bzw. Ziehen im linken unteren Bereich des Applikationsfensters generiert.
Die Variablen bedeuten:
- n1: Anzahl der Zähne des festen Zahnrades
- n2: Anzahl der Zähne des abrollenden Zahnrades
- R: Radius des festen Kreises
- r: Radius des abrollenden Kreises
- d: Abstand des Stiftes zum Mittelpunkt des abrollenden Kreises.
Die Werte der Variablen können selbstverständlich manipuliert werden.
Definition E.3: Ellipse
- Es sei
 eine Hypozykloide, für die die folgenden Bezeichnungen gelten mögen: R: Radius des festen Kreises, r: Radius des abrollenden Kreises und d: Abstand des Stiftes zum Mittelpunkt des abrollenden Kreises. Wenn ... , dann ist
eine Hypozykloide, für die die folgenden Bezeichnungen gelten mögen: R: Radius des festen Kreises, r: Radius des abrollenden Kreises und d: Abstand des Stiftes zum Mittelpunkt des abrollenden Kreises. Wenn ... , dann ist  eine Ellipse.
eine Ellipse.
- Es sei
Wenn R doppelt so groß wie r und d ungleich 0 ist, dann ist  eine Ellipse.--Geometriker 21:32, 25. Apr. 2011 (CEST)
eine Ellipse.--Geometriker 21:32, 25. Apr. 2011 (CEST)

