12)
Aus Geometrie-Wiki
Version vom 14. Dezember 2011, 13:39 Uhr von Tutorin Anne (Diskussion | Beiträge)
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  mit
mit  und
und  .
.
Vor.: Es sei  eine Strecke.
eine Strecke.
Beh.: 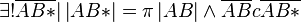
Bew.:Existenz:
| Schritt | Begründung |
|---|---|
(2) 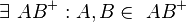 |
Def Strahl |
(3) 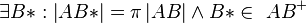 |
A vom Lineal, (2) |
(4) 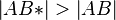 |
(3),da Abstand 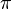 mal so groß mal so groß
|
(5) 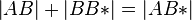 |
zw. Relation, (4),(3) |
| (6) zw(A,B,B*) | (5) |
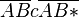 |
(6),(2),(3) |
Ein schöner Beweis.
zu Schritt 5, Begründung: Kann ich nicht ganz nachvollziehen - steht das in der Definition Zwischenrelation?--Tutorin Anne 17:29, 4. Dez. 2011 (CET)
zu Schritt 6 - Jetzt folgerst du daraus die Zwischenrelation, nutz sie vorher (5) aber schon zur Begründung -mh?--Tutorin Anne 17:29, 4. Dez. 2011 (CET)
- könnte man schritt 5 nicht so belassen und als begründung einfach anführen, dass die punkte kollinear sind und dementsprechend die dreiecksungleichung anführen?--Miriam 20:15, 5. Dez. 2011 (CET)
- Ja, das würde, denke ich, so gehen. Schritt 6 kann dann mit Definition Zwischenrelation begründet werden.--Tutorin Anne 13:39, 14. Dez. 2011 (CET)
Bew.:Eindeutigkeit:
Ann.: 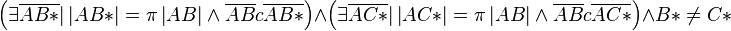
| Schritt | Begründung |
|---|---|
(1) 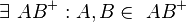 |
Def Strahl |
(2) 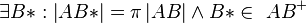 |
A vom Lineal, (1) |
(3) 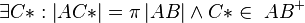 |
A vom Lineal, (1) |
(4) 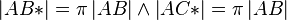 |
(2),(3) |
(5) 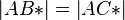 |
Rechen in R, (4) |
(6) 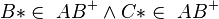 |
(2),(3) |
| (7)Fehler beim Parsen(Unbekannte Funktion „\lightning“): B* = C* \lightning zur Ann. ,diese ist zu Verwerfen | A vom Lineal (6),(4)--RicRic 13:32, 4. Dez. 2011 (CET) |
- Jetzt haben Sie gezeigt, dass es auf dem Strahl
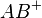 genau eine solche Strecke
genau eine solche Strecke  gibt... aber evtl. gibt es ja noch welche, die nicht auf dem Strahl liegen? Was wäre dann?--Spannagel 13:58, 10. Dez. 2011 (CET)
gibt... aber evtl. gibt es ja noch welche, die nicht auf dem Strahl liegen? Was wäre dann?--Spannagel 13:58, 10. Dez. 2011 (CET)

