Zusatzaufgaben 3 (SoSe 12)

Aufgabe 1

Beweisen Sie mit Hilfe einer Wahrheitstabelle:

$(\ A \Rightarrow B) \wedge (\ B \Rightarrow A) \Leftrightarrow (\ A \Leftrightarrow B)$

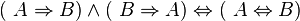
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Lösung von Zusatzaufgabe 4.1_S (SoSe_12)

Aufgabe 2

Vergleichen Sie die Wahrheitswerte von

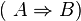$(\ A \Rightarrow B)$ und $(\ A \wedge \neg B)$.

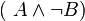Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.
Lösung von Zusatzaufgabe 4.2_S (SoSe_12)

Aufgabe 3

Das Axiom I.7 sagt aus:

Es gibt vier Punkte, die nicht komplanar sind.

Es sei $\ \epsilon$ eine beliebige Ebene und $\ A, B, C, D$ die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte $\ A, B, C, D$ mit $\ \epsilon$ auftreten können.

Lösung von Zusatzaufgabe 4.3_S (SoSe_12)

Aufgabe 4

Satz:

Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.

1. Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
2. Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
3. Beweisen Sie den Satz. Hier ein Anfang für den Beweis:

Beweis

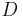Es seien $\ A, B, C$ und $\ D$ vier Punkte, die nicht komplanar sind.

zu zeigen

...

Annahme:

Es gibt drei Punkte von den vier Punkten $\ A, B, C, D$, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...

Lösung von Zusatzaufgabe 4.4_S (SoSe_12)