Lösung von Aufgabe 5.1 S (SoSe 12)
Die Aufgabe
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Lösungsvorschlag 2 (Neran69)
Lösungsvorschlag 2 von --Neran69 01:34, 18. Mai 2012 (CEST)
Beweis: Ein Pkt liegt genau zwischen den beiden anderen :
Voraussetzung: 
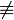

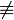


 ,
, ,
,

 (paarw. versch und koll)
Behauptung:
(paarw. versch und koll)
Behauptung:  +
+  =
=  (ein Pkt, in diesem Fall B, liegt genau zwischen A und C)
(ein Pkt, in diesem Fall B, liegt genau zwischen A und C)
Beweis d. Widerspruch:  +
+  >
>  (Annahme, Dreiecksungleichung,
(Annahme, Dreiecksungleichung, 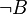 )
)

 ist Dreieck und ein Widerspruch zur Voraussetzung bzgl. koll
ist Dreieck und ein Widerspruch zur Voraussetzung bzgl. koll
 die Behauptung stimmt!
die Behauptung stimmt!
Beweis: Kein anderer Pkt liegt dazwischen
Voraussetzung: 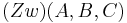 (s.o.)
Behauptung:
(s.o.)
Behauptung:  <
<  (Annahme, dass A auf jeden Fall nicht zwischen B und C liegt)
(Annahme, dass A auf jeden Fall nicht zwischen B und C liegt)
Beweis d. Widerspruch:
1.  =
= 

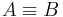 Widerspruch zur Voraussetzung bzgl. paarw. versch.
2.
Widerspruch zur Voraussetzung bzgl. paarw. versch.
2.  >
> 

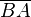 +
+  =
= 

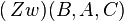 Widerspruch zur Voraussetzung
Widerspruch zur Voraussetzung 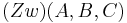
Beweis für C äquivalent
Zu Lösungsvorschlag 2 von Neran69:
Hm...Was ist die Behauptung? Sie haben die Behauptung meiner Meinung nach so verstanden: Ein Punkt liegt genau dazwischen, d.h. er liegt auf der Strecke zwischen den beiden anderen Punkten und bildet somit kein Dreieck. Das ist aber nicht gemeint! Gemeint ist: Es kann nur entweder A in der Mitte liegen, oder B oder C. Also es gilt genau EINE von den drei möglichen Zwischenrelationen. Siehe auch Hinweise von m.g.--Buchner 13:31, 18. Mai 2012 (CEST)
Lösungsvorschlag 1 (Gilmore)
Vor.: koll(A,B,C) und liegen auf einer Geraden g
Beh.: |AB| + |BC| = |AC|
Ann.: Zw(A,B,C)  Zw(C,B,A)
Zw(C,B,A)  A,B,C
A,B,C  g
g
dir.Bew.: Zw(A,B,C)
|AB| + |BC| = |AC|
|CB| + |BA| = |CA|
 Zw(A,B,C)
Zw(A,B,C)
 koll(A,B,C)
koll(A,B,C)
 A,B,C
A,B,C  g
g
Der Satz stimmt: B liegt zwischen A und C --Gilmore 18:34, 17. Mai 2012 (CEST)
Kommentar zu Lösungsvorschlag 1 von --*m.g.* 18:48, 17. Mai 2012 (CEST)
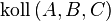 bedeutet, dass die drei Punkte auf ein und derselben Geraden liegen, alles was hinter dem und kommt ist somit "doppelt gemoppelt", also weglassen.
bedeutet, dass die drei Punkte auf ein und derselben Geraden liegen, alles was hinter dem und kommt ist somit "doppelt gemoppelt", also weglassen.
- Die Behauptung:
 spiegelt die Aussage des Satzes nicht korrekt wider:
spiegelt die Aussage des Satzes nicht korrekt wider:
- Der Satz hat eigentlich zwei Behauptungen:
- Überhaupt einer der drei kollinearen Punkte liegt zwischen den beiden anderen (Existenz),
- Kein weiterer Punkt liegt zwischen den beiden anderen. Konkreter: Wenn wir etwa mit
 den Punkt gefunden hätten der von den drei Punkten zwischen den beiden anderen (also in diesem Fall zwischen
den Punkt gefunden hätten der von den drei Punkten zwischen den beiden anderen (also in diesem Fall zwischen  und
und  ) liegt, dann liegt weder
) liegt, dann liegt weder  zwischen
zwischen  und
und  noch
noch  zwischen
zwischen  und
und  (Eindeutigkeit).
(Eindeutigkeit).
- Die Annahme von Gilmore sagt nun nichts anderes aus als: Wenn der Punkt
 zwischen den Punkten
zwischen den Punkten  und
und  liegt, dann liegt
liegt, dann liegt  auch zwischen den Punkten
auch zwischen den Punkten  und
und  . Das hat nichts mit der Aussage des Satzes zu tun.
. Das hat nichts mit der Aussage des Satzes zu tun.
- Es ist klar, dass die Beweisführung unter diesen Umständen daneben gehen muss. Am Anfang des Beweises steht, dass
 zwischen
zwischen  und
und  liegt. Warum sollte das so sein? Am Ende des Beweises ergibt sich dann, dass
liegt. Warum sollte das so sein? Am Ende des Beweises ergibt sich dann, dass ,
,  und
und drei Punkte ein und derselben Geraden sind. Das war doch die Voraussetzung des Satzes überhaupt. Wir erinnern uns: Wenn
drei Punkte ein und derselben Geraden sind. Das war doch die Voraussetzung des Satzes überhaupt. Wir erinnern uns: Wenn  ,
,  und
und  Punkte ein und derselben Geraden sind, dann ... . Also wie durch Zauber haben wir zu Anfang der Beweisführung drei Punkte von denen
Punkte ein und derselben Geraden sind, dann ... . Also wie durch Zauber haben wir zu Anfang der Beweisführung drei Punkte von denen  zwischen
zwischen  und
und  liegt und am Ende kommt heraus, dass die drei Punkte Punkte ein und derselben Geraden sind. Zusammengefasst: Wenn
liegt und am Ende kommt heraus, dass die drei Punkte Punkte ein und derselben Geraden sind. Zusammengefasst: Wenn  ,
,  und
und  Punkte ein und derselben geraden sind, dann sind
Punkte ein und derselben geraden sind, dann sind  ,
,  und
und  Punkte ein und derselben Geraden: Wieder mal: Wenn du kein iPhone hast, dann hast du kein iPhone.
Punkte ein und derselben Geraden: Wieder mal: Wenn du kein iPhone hast, dann hast du kein iPhone.
Nicht entmutigen lassen, und vor allem nicht versuchen irgendwie nach einem Algorithmus zu arbeiten. Formulieren Sie ruhig umgangssprachlich und weniger formal, das formale kommt dann schon.--*m.g.* 19:23, 17. Mai 2012 (CEST)
Ein wenig Hilfe (M.G.)
Teile und Herrsche ist ein Konzept zum Lösen von Problemen. Sie haben eigentlich zwei Probleme:
- Beweisen, dass von A, B und C einer zwischen den beiden anderen liegt.
- Beweisen, dass kein weiterer zwischen den beiden anderen liegt.
Führen Sie entsprechend auch zwei Beweise.
Erst zeigen Sie, dass überhaupt einer der drei Punkte zwischen den anderen beiden liegt, dann sagen Sie einfach, dass das der Punkt B sein möge und zweigen durch Widerspruchsbeweis, dass dann z.B. A nicht mehr zwischen B und C liegen kann. Viel Erfolg ins besondere für Neran69, der/die gerade beim Eintippen einer Lösung ist.--*m.g.* 19:40, 17. Mai 2012 (CEST)
Lösungsvorschlag 3 (Kopernikus)
Von drei paarweise verschiedenen Punkten  und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
Beweisen Sie diesen Satz.
liegt genau einer zwischen den beiden anderen.
Beweisen Sie diesen Satz.
Vor: 
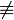

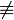
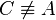

 ,
, ,
,

 (paarw. versch)
(paarw. versch)
Beh: Zw(A,B,C) oder Zw(B,C,A) oder Zw(C,A,B)
Direkter Beweis:
| Beweisschritt | Beweis | Begründung |
|---|---|---|
| I |  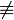  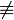 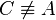   , , , ,   (paarw. versch) (paarw. versch) |
Vor: |
| II | koll(A,B,C) | def. Koll |
| III | AB| + |BC| = |AC| o.B.d.A | II, Axiom II/3 (Dreiecksungleichung)(an dieser Stelle halte ich es für besser, wenn man sagt, dass eine der Gleichungen aus Axiom II/3 gilt, da man dann im nächsten Schritt sagen kann, dass eine der drei Zwischenrelationen Zw(A,B,C)oder Zw(A,C,B) oder Zw(C,A,B) gilt. Dies entspricht dann deiner Behauptung.--Tutor Andreas 11:51, 19. Jun. 2012 (CEST) |
| IV | Zw(A,B,C) | Def. II.2 (Zwischenrelation), III, Vor. I |
| V | Beh. ist war | q.e.d |
--Kopernikus 14:19, 20. Mai 2012 (CEST)
Lösungsvorschlag 4 (RitterSport)
Ich glaube mein Lösungsvorschlag geht in ähnliche Richtung:
Vor.: koll(A,B,C) und 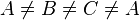
o.B.d.A nehmen wir an:
Schritt (1): |AB|+|BC|=|AC|
Das dürfen wir, wegen Axiom II/3 und der Vor. (koll(A,B,C))
daraus folgt dann Schritt (2): |AC|>|AB| und |AC|>|BC|, wegen Vor. 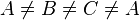 und Schritt (1))
und Schritt (1))
Schritt(3) nichtZw(A,C,B) oder nichtZw(B,A,C) (es kann weder A noch B dazwischen liegen) wegen (2)
Schritt(4) Zw(A,B,C) wegen (3)
sorry, wegen der unschönen Lesbarkeit ;)
--RitterSport 16:16, 20. Mai 2012 (CEST)
Dieses o.B.d.A. halte ich an dieser Stelle für sehr fragwürdig, da man ja erst beweisen soll, dass überhaupt eine der Gleichungen aus dem Axiom zutrifft, um dann auf die Zwischenrelation zu schließen. --Tutor Andreas 12:05, 19. Jun. 2012 (CEST) Schritt 3 kann nur aus Schritt 2 gefolgert werden, wenn Zw(A,B,C) gilt. Dies wird aber angenommen. Wie sieht es aus, wenn z.B. Zw(B,A,C) gilt? Die Lösungsidee finde ich eigentlich ganz gut, aber man sollte es noch etwas anders aufschreiben. --Tutor Andreas 12:05, 19. Jun. 2012 (CEST)
Lösungsvorschlag 5 (Wokkow)
Ich möchte im Voraus sagen, dass dies ein Lösungsvorschlag ist, aber ich wusste nicht, wie man das im Geowiki macht, ich bin nur hier hereingekommen. Und außerdem behandelt es Aufgabe 5.1. Echt sorry!
@Wokkow Passt schon, ich habe es hier her kopiert. Damit derjenige, der zunächst nur die Aufgabe haben will und nicht durch andere Lösungsvorschläge kanalisiert werden möchte, diese Möglichkeit auch bekommt, legen wie die Lösungen immer extra in eine datei, Sie brauchen nur auf den Link, der mit Lösung beginnt klicken und schon sind sie dort wo Sie hin --*m.g.* 18:04, 20. Mai 2012 (CEST)wollen.
Vorauss.: 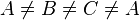 und koll(A,B,C)
Beh.: O.B.d.A. Zw(A,B,C)
und koll(A,B,C)
Beh.: O.B.d.A. Zw(A,B,C)
Beweis der Existenz:
Annahme: nicht Zw(A,B,C)
1. d.h. 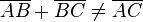
(da Annahme und Kontraposition der Zwischenrelation)
2. nkoll(A,B,C)
(da Kontraposition der Dreiecksungleichung: koll(A,B,C)O.B.d.A.
)
Widerspruch zur Voraussetzung
Beweis der Eindeutigkeit:
Vorauss.: Zw(A,B,C)
Beh.: 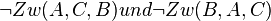 Annahme: Zw(A,C,B)
1.
Annahme: Zw(A,C,B)
1.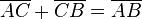
(da Annahme)
2. d.h. 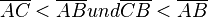 Widerspruch zur Annahme, da dort gefordert ist:
Widerspruch zur Annahme, da dort gefordert ist: 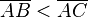
--Wokkow 12:17, 20. Mai 2012 (CEST)
Anmerkung zum Beweis von Wokkow:
Sie haben genau die richtigen Ideen gehabt! Vielleicht können Sie im zweiten Teil den Widerspruch nochmal deutlicher rausstellen, dann ist er leichter nachvollziehbar. Woher wissen Sie, dass 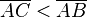 ? Welche Axiome haben Sie (wahrscheinlich unbewusst) verwendet?--Buchner 10:54, 22. Mai 2012 (CEST)
? Welche Axiome haben Sie (wahrscheinlich unbewusst) verwendet?--Buchner 10:54, 22. Mai 2012 (CEST)
Lösungsvorschlag 6 (oz44oz)
 --Oz44oz 09:00, 21. Mai 2012 (CEST)
--Oz44oz 09:00, 21. Mai 2012 (CEST)
Bei dem Beweis der Existenz dar man die Zwischenrelationen und die Gleichungen nicht mit einem mathematischen "Oder" verknüpfen, da ja sonst alle gelten könnten. Es muss ein ausschließendes "Oder" sein. Also besser "oder" in Worten schreiben.--Tutor Andreas 12:08, 19. Jun. 2012 (CEST)
Wenn man sagen will, dass drei Punkte paarweise verschieden sind, dann reicht es nicht aus, dass man 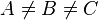 schreibt. Als Beispiel
schreibt. Als Beispiel 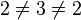 . Daran sieht man auch, dass die "Ungleich-Realtion" nicht transitiv ist. Deshalb muss man
. Daran sieht man auch, dass die "Ungleich-Realtion" nicht transitiv ist. Deshalb muss man 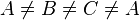 schreiben, wenn man sagen möchte, dass A,B,C paarw. verschieden sind. --Tutor Andreas 11:42, 19. Jun. 2012 (CEST)
schreiben, wenn man sagen möchte, dass A,B,C paarw. verschieden sind. --Tutor Andreas 11:42, 19. Jun. 2012 (CEST)


