Wichtige Begriffe der Geometrie - Glossar
Aus Geometrie-Wiki
Version vom 6. Juni 2010, 15:05 Uhr von Nicola (Diskussion | Beiträge)
Hier soll ein Glossar wichtiger geometrischer Begriffe und Sätze (in Bezug auf unsere Veranstaltung)entstehen. Bitte ergänzen Sie!
Grundbegriffe
- disjunkt - elementfremd, nicht gleich
- identitiv - antisymmetrisch, gleich
(z.B. wenn aRb und bRa dann a=b) --TimoRR 21:20, 5. Jun. 2010 (UTC) - inzident - beschreibt die Zugehörigkeit - Elementbezeichnung
(z.B. inzidiert ein Punkt mit einer Geraden g, wenn er zu der Geraden g gehört) --TimoRR 21:20, 5. Jun. 2010 (UTC) - kollinear - eine Gerade, die alle Punkte einer Menge enthält
- komplanar - eine Ebene, die alle Punkte einer Menge enthält --TimoRR 21:20, 5. Jun. 2010 (UTC)
- reflexiv - jedes Element steht in Relation zu sich selbst
- symmetrisch - wenn zwei Elemente in der gleichen Klasse liegen
(z.B. sind a€M und b€M, dann gilt aRb aber auch bRa) --TimoRR 21:20, 5. Jun. 2010 (UTC) - transitiv - wenn ein Element 1 zu dem nächsten Element 2 in Relation steht und das nächste
Element 2 zu dem übernächsten Element 3 in Relation steht, dann steht das Element 1 automatisch
auch in Relation zu dem übernächsten Element 3 in Relation --TimoRR 21:20, 5. Jun. 2010 (UTC)
"bitte überprüft das mal jemand ;-)"
Axiome
- Inzidenzaxiome:
AXIOM I/0
- Geraden und Ebenen sind Punktmengen.
AXIOM I/1(Axiom von der Geraden)
- Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
AXIOM I/2
- Zu jeder Geraden gibt es wenigstens zwei Punkte, die dieser Geraden angehören.
AXIOM I/3
- Es gibt wenigstens 3 Punkte, die nicht kollinear sind.
Axiom I/4
- Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält. Jede Ebene enthält (wenigstens) einen Punkt.
Axiom I/5
- Wenn zwei Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E.
Axiom I/6
- Wenn zwei Ebenen einen Punkt gemeinsam haben, so haben sie noch mindestens einen weiteren Punkt gemeinsam.
Axiom I/7
- Es gibt vier Punkte, die nicht komplanar sind.
- Abstandsaxiome:
Axiom II.1: (Abstandsaxiom)
- Zu je zwei Punkten
 und
und  gibt es eine eindeutig bestimmte nicht negative reelle Zahl
gibt es eine eindeutig bestimmte nicht negative reelle Zahl 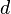 mit
mit 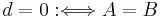 .
.
Axiom II.2:
- Für zwei beliebige Punkte
 und
und  gilt
gilt 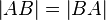 .
.
Axiom II/3: (Dreiecksungleichung)
- Für drei beliebige Punkte
 und
und  gilt:
gilt: 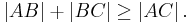
Axiom III.1: (Axiom vom Lineal)
- Zu jeder nicht negativen reelen Zahl
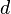 gibt es auf jedem Strahl
gibt es auf jedem Strahl  genau einen Punkt, der zum Anfangspunkt von
genau einen Punkt, der zum Anfangspunkt von  den Abstand
den Abstand 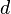 hat.
hat.
Definitionen
Definition I/2: (kollinear)
- Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
- Schreibweise: koll(A, B, C, ...) Sollten die Punkte A, B, C einer Menge nicht kollinear sein, so schreibt man:nkoll(A, B, C)
Definition I/3: (Inzidenz Punkt Ebene)
- Ein Punkt P inzidiert mit einer Ebene E, wenn P ein Element der Ebene E ist.
Definition I/4: (Inzidenz Gerade Ebene)
- Eine Gerade g gehört zu einer Ebene E, wenn jeder Punkt von g zu E gehört.
Definition I/5: (Raum)
- Die Menge aller Punkte P wird Raum genannt.
Definition I/6: (komplanar)
- Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(A, B, C, D, ...) (analog nkomp(..) für nicht komplanar)
Definition I/7: (komplanar für Geraden)
- Zwei Geraden g und h sind komplanar, wenn es eine Ebene gibt, in der beide Geraden vollständig liegen.
- Schreibweise: komp(g, h)
Definition I/8: (Geradenparallelität)
- Zwei Geraden g und h sind parallel, wenn sie identisch oder komplanar und schnittpunktfrei sind.
- In Zeichen: g||h.
Definition I/9: (windschief )
- Zwei Geraden g und h sind windschief, wenn sie schnittpunktfrei und nicht parallel sind.
Definition I/10: (parallel für Ebenen)
- Zwei Ebene E1 und E2 sind parallel, wenn sie keinen Punkt gemeinsam haben.
Definition II.1: (Abstand)
- Der Abstand zweier Punkte
 und
und  ist die Zahl, die nach dem Abstandsaxiom den Punkten
ist die Zahl, die nach dem Abstandsaxiom den Punkten  und
und  zugeordnet werden kann.
zugeordnet werden kann.
Schreibweise: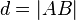 .
.
Definition II.1: (Zwischenrelation)
- Ein Punkt
 liegt zwischen zwei Punkten
liegt zwischen zwei Punkten  und
und  , wenn
, wenn  gilt und der Punkt
gilt und der Punkt  sowohl von
sowohl von  als auch von
als auch von  verschieden ist.
verschieden ist.
- Schreibweise:

Definition II.2: (Strecke, Endpunkte einer Strecke)
- Es seien
 und
und  zwei verschiedene Punkte. Die Punktmenge, die
zwei verschiedene Punkte. Die Punktmenge, die  und
und  sowie alle Punkte, die zwischen
sowie alle Punkte, die zwischen  und
und  liegen, enthält, heißt Strecke
liegen, enthält, heißt Strecke  . Stimmt das? --Sternchen 13:07, 5. Jun. 2010 (UTC)
. Stimmt das? --Sternchen 13:07, 5. Jun. 2010 (UTC)
- Es seien
Definition II.3: (Länge einer Strecke)
- Es seien
 und
und  zwei verschiedene Punkte. Der Abstand
zwei verschiedene Punkte. Der Abstand 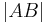 heißt Länge der Strecke
heißt Länge der Strecke  . OK? --Sternchen 13:09, 5. Jun. 2010 (UTC)
. OK? --Sternchen 13:09, 5. Jun. 2010 (UTC)
- Es seien
Definition II.3: (Halbgerade, bzw. Strahl)
Definition III.1: (Mittelpunkt einer Strecke)
- Wenn ein Punkt
 der Strecke
der Strecke  zu den Endpunkten
zu den Endpunkten  und
und  jeweils den selben Abstand hat, dann ist er der Mittelpunkt der Strecke
jeweils den selben Abstand hat, dann ist er der Mittelpunkt der Strecke  .
.
Sätze
Satz I.1
- Es seien g und h zwei Geraden. Wenn g und h nicht identisch sind, haben sie höchstens einen Punkt gemeinsam.
Satz I.2: (Kontraposition von Satz I.1)
- Es seien g und h zwei Geraden.
- Wenn g und h mehr als einen Punkt gemeinsam haben, so sind g und h identisch.
Satz I.3: (Existenz von drei Geraden)
- Es existieren mindestens drei paarweise verschiedene Geraden.
Satz I.5:
- Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
Satz I.6:
- Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
Satz I.7:
- Jede Ebene enthält (wenigstens) drei Punkte.
Satz II.1
- Aus
 folgt
folgt 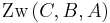 .
.
Satz II.2:
- Aus
 folgt
folgt  .
.
Satz II.3
- Es sei
 mit
mit  sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt oder
oder 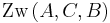 oder
oder 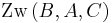 .
.
Satz II.4
- Es sei
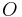 ein Punkt einer Geraden
ein Punkt einer Geraden  .
.
Die Teilmengen Fehler beim Parsen(Unbekannte Funktion „\set“): \ OA^+ \set minus \left\{ O \right\}
, 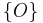 und
und 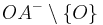 bilden eine Klasseneinteilung der Geraden
bilden eine Klasseneinteilung der Geraden  .
.
Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke)
- Jede Strecke hat genau einen Mittelpunkt.

