Serie 11 (WS 12 13)
Inhaltsverzeichnis |
Aufgabe 11.01
Formulieren Sie die Umkehrung des Basiswinkelsatzes.
Aufgabe 11.02
Es seien  drei nicht kollineare Punkte. Die Winkel
drei nicht kollineare Punkte. Die Winkel 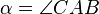 und
und 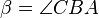 seien kongruent zueinander.
seien kongruent zueinander.
Behauptung:
Ergänzen Sie den folgenden Beweis
(H) Hilfskonstruktion:
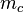 sei die Mittelsenkrechte der Strecke
sei die Mittelsenkrechte der Strecke  .
.
Begründung, dass die Hilfskonstruktion angewendet werden kann:
.................................................
Was wäre wenn
Wenn die Mittelsenkrechte 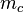 durch
durch  gehen würde, wären die Strecken
gehen würde, wären die Strecken 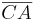 und
und 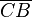 kongruent zueinander.
kongruent zueinander.
Begründung hierfür:
..................................................
Was wäre wenn nicht
Annahme: 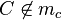
| Nr. | Beweischritt | Begründung |
|---|---|---|
| (1) | 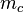 schneidet o.B.d.A. schneidet o.B.d.A. 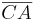 in einem Punkt, den wir in einem Punkt, den wir 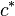 nennen wollen nennen wollen |
... |
| (2) | 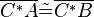 |
... |
| (3) | 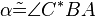 |
... |
| (4) | 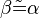 |
... |
| (5) | 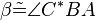 |
... |
Der Rest schreiben wir als kleinen Aufsatz:
Die beiden Winkel  und
und 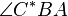 sind also nach der bisherigen Beweisführung kongruent bzw. haben dieselbe Größe.
sind also nach der bisherigen Beweisführung kongruent bzw. haben dieselbe Größe.
Weil sie auch den Schenkel 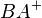 gemeinsam haben und
gemeinsam haben und  und
und 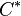 in derselben Halbebene bzgl.
in derselben Halbebene bzgl.  liegen,
liegen,
müssen die die Schenkel 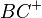 und
und 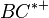 nach dem ... identisch sein.
nach dem ... identisch sein.
Wegen dieser Identität der beiden Strahlen 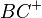 und
und 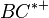 und weil
und weil  der Schnittpunkt von
der Schnittpunkt von 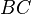 mit
mit 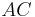 und
und 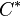 der Schnittpunkt von
der Schnittpunkt von 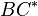 mit
mit 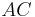 ist, sind ..... identisch.
ist, sind ..... identisch.
Wegen dieser Identität geht die Mittelsenkrechte 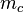 durch den Punkt
durch den Punkt  . Wir haben uns schon überlegt, dass in diesem Fall
. Wir haben uns schon überlegt, dass in diesem Fall 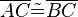 gilt. q.e.d.
gilt. q.e.d.
Aufgabe 11.03
Es sei  ein Winkel mit den Schenkeln
ein Winkel mit den Schenkeln  und
und  und dem Scheitel
und dem Scheitel  . Ferner sei
. Ferner sei  die Winkelhalbierende von
die Winkelhalbierende von  , also ein Strahl im Inneren von
, also ein Strahl im Inneren von  , der als Anfangspunkt S hat und
, der als Anfangspunkt S hat und  in zwei kongruente Teilwinkel
in zwei kongruente Teilwinkel 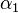 und
und 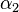 teilt. Auf
teilt. Auf  sei ein beliebiger von
sei ein beliebiger von  verschiedener Punkt
verschiedener Punkt  gegeben.
gegeben. 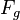 sei der Fußpunkt des Lotes von
sei der Fußpunkt des Lotes von  auf
auf  :
:
Wir konstruieren jetzt auf dem Schenkel  den Punkt
den Punkt 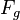 , indem wir auf
, indem wir auf  den Abstand
den Abstand 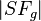 abtragen:
abtragen:
Beweisen Sie: 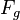 ist der Fußpunkt des Lotes von
ist der Fußpunkt des Lotes von  auf
auf  .
.
Aufgabe 11.04
Definieren Sie: Abstand eines Punktes  zu einer Geraden
zu einer Geraden  :
:
Aufgabe 11.05
Ergänzen Sie die folgende Implikation:
Wenn ein Punkt P zur Winkelhalbierenden des Winkels  gehört, dann hat er zu den Schenkeln von
gehört, dann hat er zu den Schenkeln von  .......
.......
Aufgabe 11.06
Es sei  ein Punkt aus dem Inneren des Winkels
ein Punkt aus dem Inneren des Winkels  . Der Scheitel von
. Der Scheitel von  sei der Punkt
sei der Punkt  . P möge zu den Schenkeln von
. P möge zu den Schenkeln von  jeweils denselben Abstand haben. Beweisen Sie:
jeweils denselben Abstand haben. Beweisen Sie: 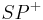 ist die Winkelhalbierende von
ist die Winkelhalbierende von  . Tip: Ssw hilft.
. Tip: Ssw hilft.
Lösung Aufgabe 11.06 WS_12_13 ...jeweils ein und denselben Abstand.
Aufgabe 11.07
Die Implikationen aus 11.05 und 11.06 lassen sich zu einer Äquivalenz zusammenfassen:
Ein beliebiger Punkt  aus dem Inneren eines Winkels
aus dem Inneren eines Winkels  ist genau dann ein Punkt der Winkelhalbierenden von
ist genau dann ein Punkt der Winkelhalbierenden von  , wenn .......
, wenn .......
Aufgabe 11.08
Beweisen Sie die folgenden Korollare aus dem ´schwachen Außenwinkelsatz:
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Korollar 2 zum schwachen Außenwinkelsatz
- Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180.
Korollar 3 zum schwachen Außenwinkelsatz
- Sollte ein Dreieck rechtwinklig sein, dann ist der rechte Winkel der größte aller Innenwinkel dieses Dreiecks.
Aufgabe 11.09
Beweisen Sie: (Existenz und Eindeutigkeit des Lotes)
- Zu jedem Punkt
 außerhalb einer Geraden
außerhalb einer Geraden  gibt es genau ein Lot von
gibt es genau ein Lot von  auf
auf  .
.
- Zu jedem Punkt
Aufgabe 11.10
Wir beziehen uns auf den Beweis des schwachen Außenwinkelsatzes aus der Vorlesung vom 18. Januar 2013.
Der Punkt P sei in der beschriebenen Art und Weise konstruiert.
Es blieb zu zeigen, dass  im Inneren von
im Inneren von 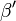 liegt. Was das bedeutet ist klar:
liegt. Was das bedeutet ist klar:
Teil 1 war einfach, wir haben  ja schließlich so konstruiert.
ja schließlich so konstruiert.
Teil 2 hätten wir auch dann gezeigt, wenn wir nachweisen, dass  im Inneren von des Winkels
im Inneren von des Winkels 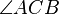 liegt. Das Innere von
liegt. Das Innere von 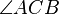 ist schließlich nichts anderes als die Schnittmenge der beiden Halbebene
ist schließlich nichts anderes als die Schnittmenge der beiden Halbebene 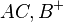 und
und 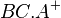 . Von diesen beiden Halbebenen interessiert uns eigentlich nur
. Von diesen beiden Halbebenen interessiert uns eigentlich nur 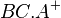 . Aber gut, wenn
. Aber gut, wenn  im Inneren von
im Inneren von 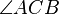 liegen würde, dann würde
liegen würde, dann würde  natürlich auch in
natürlich auch in 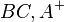 liegen.
liegen.
Beweisen unter Verwendung der Lemmata zu Winkeln, dass  im Inneren von des Winkels
im Inneren von des Winkels 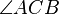 liegt.
liegt.