Übung Aufgaben 12 (WS 12 13)
Inhaltsverzeichnis |
Aufgabe 12.1
Durch welche Abbildung kann die Verkettung zweier Punktspiegelungen ersetzt werden? Begründen Sie!
Lösung von Aufgabe 12.1P (WS_12_13)
Aufgabe 12.2
Zeigen Sie, dass die Verkettung dreier Punktspiegelungen wieder eine Punktspiegelung ist.
Lösung von Aufgabe 12.2P (WS_12_13)
Aufgabe 12.3
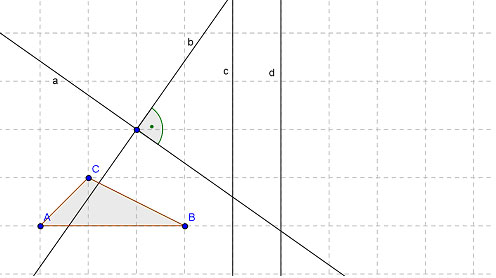
Gegeben sei ein Dreieck  und die Geraden a, b, c und d mit:
und die Geraden a, b, c und d mit: 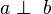 und
und 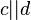 entsprechend der Skizze.
entsprechend der Skizze.
- Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen
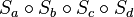 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
- Konstruieren Sie oben in der Skizze das Bild des Dreiecks
 , das nach der Verkettung
, das nach der Verkettung 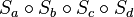 entsteht, mit Hilfe der Ersatzabbildung.
entsteht, mit Hilfe der Ersatzabbildung.
Lösung von Aufgabe 12.3P (WS_12_13)
Aufgabe 12.4
Zeigen Sie, dass die Verkettung einer Drehung 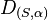 mit einer Verschiebung wieder eine Drehung
mit einer Verschiebung wieder eine Drehung 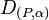 ergibt. Wo liegt das neue Drehzentrum P?
ergibt. Wo liegt das neue Drehzentrum P?
Lösung von Aufgabe 12.4P (WS_12_13)
Aufgabe 12.5
Das Dreieck  wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!
wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!