Diskussion:Halbebenen oder das Axiom von Pasch
Inhaltsverzeichnis |
Analogiebetrachtungen bezüglich des Begriffes der Halbebene
alte Version 21:28, 23. Jun. 2010 (UTC)
| |
|
 , das in Klassen eingeteilt wird , das in Klassen eingeteilt wird | |
 ist eine Gerade ist eine Gerade
|
 ist eine Ebene ist eine Ebene
|
 | |
| eindimensional | zweidimensional |
 , das , das  in Klassen einteilt in Klassen einteilt | |
| Anfangspunkt A | Bezugspunkt P |
 | |
| eindimensional | eindimensional |
 teilt teilt 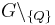 in genau zwei Klassen in genau zwei Klassen | |
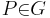 , die mit , die mit  bezüglich bezüglich  „auf derselben Seite liegen“ „auf derselben Seite liegen“ | |
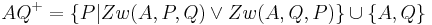
|
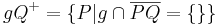
|
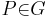 , die bezüglich , die bezüglich  nicht auf der Seite von nicht auf der Seite von  liegen. liegen. | |
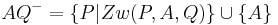
|
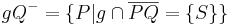
|

BITTE NOCHMAL ÜBERPRÜFEN --TimoRR 11:31, 22. Jun. 2010 (UTC)
Bemerkungen zu den Analogieüberlegungen --*m.g.* 19:18, 17. Jun. 2010 (UTC)
- Wird in beiden Fällen wirklich eine Gerade in Klassen eingeteilt? Erhalten wir eine Halbebene dadurch, dass wir eine Gerade in Klassen einteilen? CHECK
- Dimension: Gemeint ist, welche Dimension das Objekt hat, welches in Klassen bzw. Teilmengen eingeteilt wird. Ein räumliches Objekt, wie etwa ein Würfel hat die Dimension drei, ein Quadrat liegt vollständig in einer Ebene und ist deshalb ein zweidimensionales Objekt. Eine Strecke liegt auf einer Geraden und ist deshalb ein eindimensionales geometrisches Objekt. Wir haben es bei unseren beiden Begriffen Halbgerade und Halbebene einmal mit einem 1D- und einmal mit einem 2D-Begriff zu tun. Den Begriff der Dimension verwenden wir hier intuitiv, ohne ihn definiert zu haben. CHECK
- Halbgerade: Eine Gerade wird in zwei Halbgeraden eingeteilt. Was für ein Objekt bewirkt diese Einteilung? Eine Halbgerade oder nicht doch eher ein Punkt, der Anfangspunkt der beiden Halbgeraden? Eine Ebene läßt ich auf unendlich viele Arten in genau zwei Halbenen zerlegen. Was für ein Objekt ist verantwortlich dafür, dass wir eine Einteilung in zwei spezielle Halbebenen bekommen? Was ist das Analogon zum Anfangspunkt zweier entgegengesetzter Strahlen bezüglich der Einteilung einer Ebene in zwei Halbebene, deren Vereinigungsmenge wieder die Ausgangebene ergibt? CHECK
- Die Definitionen zu den beiden Halbgeraden
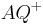 und
und 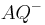 sind korrekt. Die Analogie zum problem der Halbebenen wird aber besser verdeutlich, wenn man diese Definitionen anders formuliert und sich dabei explizit auf die Strecke
sind korrekt. Die Analogie zum problem der Halbebenen wird aber besser verdeutlich, wenn man diese Definitionen anders formuliert und sich dabei explizit auf die Strecke 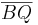 bezieht. Die Idee, Halbgeraden über die Strecke
bezieht. Die Idee, Halbgeraden über die Strecke  zu definieren lag der Übungsaufgabe 7.4 Lösung_von_Aufgabe_7.4 zugrunde. Die Definition habe ich zu Beginn meiner Vorlesung vom 11.06. erläutert.
zu definieren lag der Übungsaufgabe 7.4 Lösung_von_Aufgabe_7.4 zugrunde. Die Definition habe ich zu Beginn meiner Vorlesung vom 11.06. erläutert.
Meinen sie wirklich BQ oder PQ, wenn PQ, dann CHECK - Die Definition der Halbebenen ist prinzipiell richtig. Nach stillschweigender Konvention kennzeichnen wir jedoch Punkte durch große lateinische Buchstaben. Also nicht
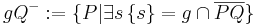 sondern
sondern 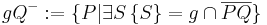 CHECK
CHECK
Definition IV.1: (offene Halbebene), alte Version
Definition IV.1: (offene Halbebene)
- Es sei
 eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Teilmengen der Ebene
versteht man die folgenden Teilmengen der Ebene  ohne die Gerade
ohne die Gerade  :
:
- Es sei
Kommentar von --*m.g.* 20:51, 23. Jun. 2010 (UTC)
TimoRR und Principella, Sie haben völlig recht. So wie die Sache momentan formuliert ist, ist 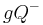 die Menge aller Punkte
die Menge aller Punkte  , die die Eigenschaft haben, dass die Strecke
, die die Eigenschaft haben, dass die Strecke  einen gemeinsamen Punkt mit der Geraden
einen gemeinsamen Punkt mit der Geraden  hat. Dieser gemeinsame Punkt existiert insbesondere auch dann, wenn einer der beiden Endpunkte
hat. Dieser gemeinsame Punkt existiert insbesondere auch dann, wenn einer der beiden Endpunkte  oder
oder  auf
auf  liegt. Letzteres schließt die "Präambel" der Definition offene Halbebene aus:
liegt. Letzteres schließt die "Präambel" der Definition offene Halbebene aus:
Es sei  eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Dem Punkt  wurde selbiges nicht verboten. Damit haben Sie recht: Momentan wird die echte Halbebene
wurde selbiges nicht verboten. Damit haben Sie recht: Momentan wird die echte Halbebene 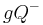 definiert, dh. die Trägergerade
definiert, dh. die Trägergerade  ist mit dabei.
ist mit dabei.
Sie haben jetzt verschiedene Möglichkeiten dieses zu bereinigen:
- Sie schreiben das Verbot, dass
 nicht auf
nicht auf  liegen darf in die Präambel der Definition:
liegen darf in die Präambel der Definition:
Es sei eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Teilmengen der Ebene
versteht man die folgenden Teilmengen der Ebene  ohne die Gerade
ohne die Gerade  : ...
: ...
- Sie behalten die derzeitige Definition
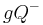 bei, hängen aber einen Zusatz an, der die Gerade
bei, hängen aber einen Zusatz an, der die Gerade  wieder raus nimmt:
wieder raus nimmt: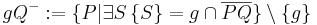
- Sie sprechen das Verbot in der geschweiften Klammer der Mengendefinition aus:
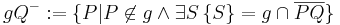
Beweis des Satzes IV.1, alte Version
Beweis des Satzes IV.1
Voraussetzung: 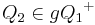
Behauptung: 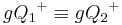 und
und 
| Schritt | Aussage | Begründung |
| (1) | 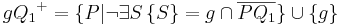 Die Strecke 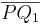 schneidet nicht die Trägergerade g. schneidet nicht die Trägergerade g. |
Definition von Halbebene |
| (2) | 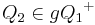 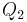 liegt in der Halbebene liegt in der Halbebene 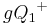 |
Voraussetzung |
| (3) | 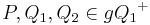 |
Schritt (1) und (2) |
| (4) | Die Strecke 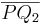 schneidet nicht die Trägergerade g. schneidet nicht die Trägergerade g. |
Schritt (3), Definition von Halbebene |
| (5) | 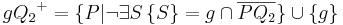 |
Schritt (4) |
| (6) | Es gilt: 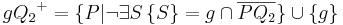 und und
| |
| (7) | 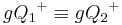 |
Der Definitionsbereich der beiden Halbebene ist identisch - Schritt (6) |
| (8) |  |
Die Mengen 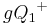 und und 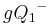 sind disjunkt, gleiches gilt für die Mengen sind disjunkt, gleiches gilt für die Mengen 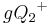 und und 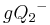 Schritt (7) - Durch Umformung: Schritt (7) - Durch Umformung:
|
Stimmt das so? --Heinzvaneugen 12:23, 23. Jun. 2010 (UTC)
Also, Punkt (4) ist ja eigentlich das, was Sie zeigen wollen, denn wenn die Strecke 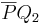 die Trägergerade g nicht schneidet, dann gilt dies ja für jedes beliebige
die Trägergerade g nicht schneidet, dann gilt dies ja für jedes beliebige 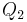 und das heißt, dass Sie statt
und das heißt, dass Sie statt 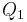 auch
auch 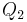 als Repräsentanten ihrer Halbebene nehmen können. Soweit so gut, allerdings können Sie das nicht einfach aus der Definition der Halbebene schließen, weil sie diesen Zusammenhang ja erst noch zeigen müssen (typischer Fall eines Zirkelschlusses). Sie kommen nicht umhin, das Axiom von Pasch an dieser Stelle mit einzubeziehen! Damit wir Pasch verwenden dürfen, müssen wir allerdings voraussetzen, dass P,
als Repräsentanten ihrer Halbebene nehmen können. Soweit so gut, allerdings können Sie das nicht einfach aus der Definition der Halbebene schließen, weil sie diesen Zusammenhang ja erst noch zeigen müssen (typischer Fall eines Zirkelschlusses). Sie kommen nicht umhin, das Axiom von Pasch an dieser Stelle mit einzubeziehen! Damit wir Pasch verwenden dürfen, müssen wir allerdings voraussetzen, dass P, 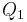 und
und 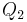 nicht kollinear sind. Der kollineare Fall ist dann nochmal getrennt zu untersuchen, lässt sich dann aber über die Zwischenrelation und über Teilmengenbeziehungen leicht beweisen.--Schnirch 13:59, 23. Jun. 2010 (UTC)
nicht kollinear sind. Der kollineare Fall ist dann nochmal getrennt zu untersuchen, lässt sich dann aber über die Zwischenrelation und über Teilmengenbeziehungen leicht beweisen.--Schnirch 13:59, 23. Jun. 2010 (UTC)
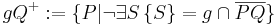
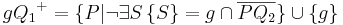 || Voraussetzung und Schritt (5)
|| Voraussetzung und Schritt (5)


 gilt somit auch
gilt somit auch 
