Übung Aufgaben 9 (SoSe 13)

Aufgabe 9.1

Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
Lösung von Aufgabe 9.1P (SoSe_13)

Aufgabe 9.2

Beweisen Sie die Geradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue der Geradenspiegelung.
Lösung von Aufgabe 9.2P (SoSe_13)

Aufgabe 9.3

Beweisen Sie die Winkeltreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue und die Eigenschaft der Geradenspiegelung winkelmaßerhaltend zu sein.
Lösung von Aufgabe 9.3P (SoSe_13)

Aufgabe 9.4

m sei Mittelsenkrechte der Strecke $\overline{AB}$. Beweisen Sie durch Kontraposition: $\left| AP \right| =\left| BP \right|\Rightarrow P\in m$
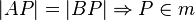
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.
Lösung von Aufgabe 9.4P (SoSe_13)