Lösung von Aufgabe 11.4P (SoSe 13)
Aus Geometrie-Wiki
Version vom 12. Juli 2013, 14:34 Uhr von Blumenkind (Diskussion | Beiträge)
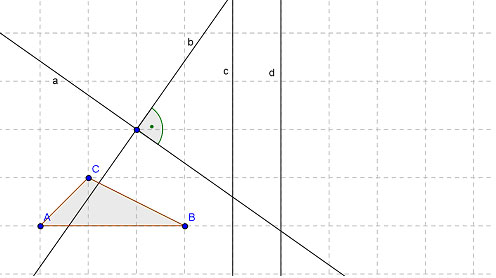
Gegeben sei ein Dreieck  und die Geraden a, b, c und d mit:
und die Geraden a, b, c und d mit: 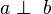 und
und 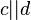 entsprechend der Skizze.
entsprechend der Skizze.
- Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen
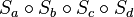 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
- Konstruieren Sie oben in der Skizze das Bild des Dreiecks
 , das nach der Verkettung
, das nach der Verkettung 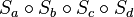 entsteht, mit Hilfe der Ersatzabbildung.
entsteht, mit Hilfe der Ersatzabbildung.
Ich probier es mal bin mir aber nicht sicher, ob es richtig ist.
Da bei mir leider kein Geogebra funktioniert versuche ich es irgendwie mit Sätzen;-).
Also: Eine Verkettung von vier Spiegelgeraden kann durch 2 Spiegelgeraden ersetzt werden. Falls sich die Geraden scheiden--> DREHUNG bzw. sind sie parallel--> VERSCHIEBUNG Kursiver Text
- Zuerst habe ich eine Parallele zu c durch S gezogen und die gerade c` genannt mit c`II c und c´geschnitten b =(S).
- Ebenso wissen wir dass es eine weitere Gerade gibt mit d` zu c` c und d da diese drei Geraden parallel zueinander sind.
- Für d`gilt: Sc o Sd= Sc´o Sd´
== Kursiver Text ==
 Sa o Sb o Sc o Sd
Sa o Sb o Sc o Sd
- = Sa o Sb o Sc´o Sd´ ich habe die FORMEL die ich für d´geschrieben habe ersetzt einfach
- = (Sa o Sb o Sc´) o Sd´ ich habe es in die Klammer zusammengefügt, da alle drei Geraden durch den selben Punkt S gehen. Bzw. zusammengefasst
- = Sx o Sd´ (2) und Sx ist die neue Spiegelung
- Daraus folgt das man eine Verkettung von 4 Geraden durch 2 ersetzen kann. --Blumenkind 15:34, 12. Jul. 2013 (CEST)Blumenkind 15:32, 12. Juli