Lösung von Aufg. 6.3P (SoSe 13)

Definieren Sie den Begriff: "konvexe Punktmenge" indem Sie die verbal formulierte Definition (siehe Wiki-Skript) in eine geeignete "Mengenschreibweise" übersetzen.
M ist konvex, wenn gilt: ...

• (M/ A ist Element M und B ist Element M) vereinigt mit der Strecke AB und Die Strecke AB ist Element M--Blumenkind 13:29, 1. Jun. 2013 (CEST)Blumenkind 13:29, 1.6.13
  • Ich verstehe ehrlich nicht genau, was du damit sagen willst. So ist die Definition nicht richtig. Nutzt bitte auch die Formeln des Formeleditor (Symbol ganz links mit dem Summenzeichen).--Tutorin Anne 18:48, 2. Jun. 2013 (CEST)
    • M ist konvex wenn gilt: 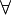$\forall$ A, B $\in$ M und die Strecke AB ist eine echte Teilmenge von M.--Blumenkind 16:38, 3. Jun. 2013 (CEST)Blumenkind 16:38, 3. Juni
    • $M$ ist konvex, wenn gilt: $\forall A, B \in M \wedge \overline{AB}\subset M.$
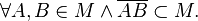
      • So sieht das in Formelschreibweise aus. Die Definition stimmt so noch nicht ganz. Kopiert die Aussage und verbessert diese dann. --Tutorin Anne 19:45, 5. Jun. 2013 (CEST)
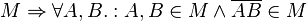        • $M \Rightarrow \forall A,B.: A,B \in M \wedge \overline{AB} \in M$--Beencken 19:37, 9. Jun. 2013 (CEST)
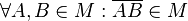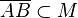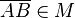        • M ist konvex, wenn gilt: $\forall A,B \in M : \overline{AB} \in M$ - die Punkte A, B nicht doppelt nennen! Bei beiden Definitionen ist das UND nicht korrekt und es ist weder richtige $\overline{AB}\subset M$ noch $\overline{AB}\in M$ zu schreiben.Was muss also noch korregiert werden?--Tutorin Anne 09:02, 11. Jun. 2013 (CEST)

M ist konvex wenn gilt, dass M auch Teilmenge der Verbindungen ihrer enthaltenen Punkte ist. --Wüstenfuchs 16:38, 10. Jul. 2013 (CEST)

• Die Definition ist nicht korrekt. Weshalb?--Tutorin Anne 17:19, 12. Jul. 2013 (CEST)