Lösung von Zusatzaufgabe 5.1 P (SoSe 13)
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 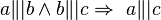 .
.
VSS: aTEILTb und bTEILTc
Beh: aTEILTC
Annahme: aTEILTNICHTc
- dieses Zeichen heißt parallel zu (das ist eine Relation) und nicht TEILT--Tutorin Anne 18:30, 2. Jun. 2013 (CEST)
BEWEIS:
1. a geschnitten c = {S} -------------------> ANNAHME
2. S ist Element von a und ---------------> (1.)
S ist Element von c
3. a und c sind jeweils parallele Geraden zu b und a und c gehen beide durch S -----------> (1.) (2.)
4. Annahme ist zu verwerfen, da Wiederspruch zum Parallelenaxiom -------------> ( 3.) Def. Parallenaxiom und wenn a durch S parallel zu b ist, dann kann nicht c durch S ebenso parallel zu b sein
---> Behauptung stimmt--Blumenkind 11:37, 31. Mai 2013 (CEST)Blumenkind 11:36, 31. Mai
b) Welche Eigenschaft der Relation  auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
---> TRANSITIVITÄT --Blumenkind 11:37, 31. Mai 2013 (CEST)Blumenkind 11:37, 31. Mai
Voraussetzung: 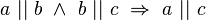
Das gehört nicht in die Vors.: mit 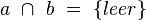 \ ,\ \ b\ \cap\ c\ =\ \left\{ {leer} \right\}
\ ,\ \ b\ \cap\ c\ =\ \left\{ {leer} \right\}
Behauptung: 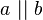
Das gehört nicht in die Vors.: 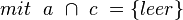
Annahme: 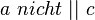
Das kansnt du dir auch sparen, da du es ja in Schritt 1 nennst: 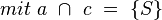
--Nolessonlearned 13:34, 16. Jul. 2013 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 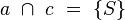
|
Annahme |
| 2) | 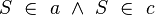
|
(1); Annahme |
| 3) | 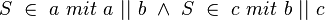
|
(2); Voraussetzung; |
| 4) | Fehler beim Parsen(Lexikalischer Fehler): a\ ||\ c\ | Widerspruch zum Parallelenaxiom;
Annahme ist zu verwerfen; Behauptung stimmt. |
Ich würde gerne genauer begründet haben, was da jetzt der Widerspruch zum Parallelenaxiom ist. Das habe ich nicht nachvollziehen können. Der Beweis geht aber sicher in die richtige Richtung.--Tutorin Anne 14:36, 16. Jul. 2013 (CEST)

