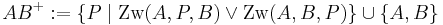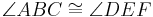Wichtige Begriffe der Geometrie - Glossar
Hier soll ein Glossar wichtiger geometrischer Begriffe und Sätze (in Bezug auf unsere Veranstaltung) entstehen. Bitte ergänzen Sie!
Grundbegriffe (undefinierte Begriffe)
- Punkt
- Gerade
- Ebene
Begriffsklärungen
- disjunkt - elementfremd, nicht gleich
- identitiv - antisymmetrisch, gleich
(z.B. wenn aRb und bRa dann a=b) --TimoRR 21:20, 5. Jun. 2010 (UTC) - inzident - beschreibt die Zugehörigkeit - Elementbezeichnung
(z.B. inzidiert ein Punkt mit einer Geraden g, wenn er zu der Geraden g gehört) --TimoRR 21:20, 5. Jun. 2010 (UTC) - kollinear - eine Gerade, die alle Punkte einer Menge enthält
- komplanar - eine Ebene, die alle Punkte einer Menge enthält --TimoRR 21:20, 5. Jun. 2010 (UTC)
- reflexiv - jedes Element steht in Relation zu sich selbst
- symmetrisch - wenn zwei Elemente in der gleichen Klasse liegen
(z.B. sind a€M und b€M, dann gilt aRb aber auch bRa) --TimoRR 21:20, 5. Jun. 2010 (UTC) - transitiv - wenn ein Element 1 zu dem nächsten Element 2 in Relation steht und das nächste
Element 2 zu dem übernächsten Element 3 in Relation steht, dann steht das Element 1 automatisch
auch in Relation zu dem übernächsten Element 3 in Relation --TimoRR 21:20, 5. Jun. 2010 (UTC)
"bitte überprüft das mal jemand ;-)"
- Das Problem ist, dass diese Erklärungen maximal Erinnerungsstützen sein können. Um auf der sicheren Seite zu sein, sollten Sie die Erkärungen in saubere Definitionen fassen.
Beispiel: Definition:(disjunkt)
Zwei Mengen und
und  sind disjunkt zueinander, wenn sie keine gemeinsamen Elemente haben.
sind disjunkt zueinander, wenn sie keine gemeinsamen Elemente haben.
- Aus meiner Sicht wäre es sinnvoll, wenn Sie diesen Abschnitt umbenennen in Basiswissen: Definitionen/Sätze und einen neuen Abschnitt zu den Erklärungen aufmachen. Dieser neue Abschnitt könnte dann Dinge beinhalten, die mehr oder weniger Prozeßwissen beinhalten. Ein Beispiel:
- Nichtfolgerbarkeit einer Aussage
 aus einer Menge
aus einer Menge  von Axiomen
von Axiomen
- Mitunter möchte man wissen, ob sich eine bestimmte Aussage
 aus einer Menge
aus einer Menge  von Axiomen folgern läßt. Gelingt uns diese Folgerung, ist alles in Ordnung. Falls diese Folgerung nicht gelingt, haben wir ein Problem: Wir können uns nicht sicher sein, ob die Folgerung prinzipiell nicht möglich ist, oder ob es unser Unvermögen war, welches das Projekt Folgerung von
von Axiomen folgern läßt. Gelingt uns diese Folgerung, ist alles in Ordnung. Falls diese Folgerung nicht gelingt, haben wir ein Problem: Wir können uns nicht sicher sein, ob die Folgerung prinzipiell nicht möglich ist, oder ob es unser Unvermögen war, welches das Projekt Folgerung von  aus
aus  scheitern ließ. Abhilfe bringt ggf. die Suche nach Modellen für
scheitern ließ. Abhilfe bringt ggf. die Suche nach Modellen für  . In jedem Modell für
. In jedem Modell für  müssen auch alle Folgerunge gelten, die aus
müssen auch alle Folgerunge gelten, die aus  abgeleitet werden können. Sollten wir nun ein Modell für
abgeleitet werden können. Sollten wir nun ein Modell für  finden, in dem
finden, in dem  nicht gilt ...
nicht gilt ...
- Mitunter möchte man wissen, ob sich eine bestimmte Aussage
- Modell für eine Menge von Axiomen
- ...
*m.g.* 12:32, 9. Jun. 2010 (UTC)
Klasseneinteilung
- Es sei
 eine Menge und
eine Menge und 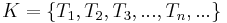 eine Menge von Teilmengen von
eine Menge von Teilmengen von  .
.
 ist eine Klasseneinteilung von
ist eine Klasseneinteilung von  , wenn gilt:
, wenn gilt:
- notwendige Bedingung 1: Keine der Teilmengen ist die leere Menge.
- notwendige Bedingung 2: Je zwei Teilmengen sind disjunkt.
- notwendige Bedingung 3: Die Vereinigung aller Teilmengen ergibt wieder die Menge
 .
.
- Mengen sind disjunkt, wenn die Schnittmenge dieser Mengen die leere Menge ist, bzw. die Mengen keine gemeinsamen Objekte besitzen.
Relationen
Definition: (n-stellige Relation)
- Es seien
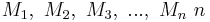 Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus
Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus 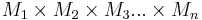 ist eine
ist eine 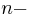 stellige Relation.
stellige Relation.
Definition: (Äquivalenzrelation)
- Eine Relation
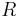 in einer Menge
in einer Menge  heißt Äquivalenzrelation, wenn sie reflexiv, symmetrisch und transitiv ist.
heißt Äquivalenzrelation, wenn sie reflexiv, symmetrisch und transitiv ist.
Axiome
- Inzidenzaxiome:
Axiom I/0
- Geraden und Ebenen sind Punktmengen.
Axiom I/1(Axiom von der Geraden)
- Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
Axiom I/2
- Zu jeder Geraden gibt es wenigstens zwei Punkte, die dieser Geraden angehören.
Axiom I/3
- Es gibt wenigstens 3 Punkte, die nicht kollinear sind.
Axiom I/4
- Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält. Jede Ebene enthält (wenigstens) einen Punkt.
Axiom I/5
- Wenn zwei Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E.
Axiom I/6
- Wenn zwei Ebenen einen Punkt gemeinsam haben, so haben sie noch mindestens einen weiteren Punkt gemeinsam.
Axiom I/7
- Es gibt vier Punkte, die nicht komplanar sind.
- Abstandsaxiome:
Axiom II.1: (Abstandsaxiom)
- Zu je zwei Punkten
 und
und  gibt es eine eindeutig bestimmte nicht negative reelle Zahl
gibt es eine eindeutig bestimmte nicht negative reelle Zahl 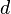 mit
mit 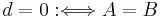 .
.
Axiom II.2:
- Für zwei beliebige Punkte
 und
und  gilt
gilt 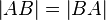 .
.
Axiom II/3: (Dreiecksungleichung)
- Für drei beliebige Punkte
 und
und  gilt:
gilt: 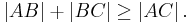
- Falls
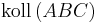 , dann ist eine der folgenden Gleichungen erfüllt:
, dann ist eine der folgenden Gleichungen erfüllt:
- Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind
 ,
,  und
und  kollinear.
kollinear.
Axiom III.1: (Axiom vom Lineal)
- Zu jeder nicht negativen reelen Zahl
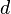 gibt es auf jedem Strahl
gibt es auf jedem Strahl  genau einen Punkt, der zum Anfangspunkt von
genau einen Punkt, der zum Anfangspunkt von  den Abstand
den Abstand 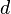 hat.
hat.
Axiom III.2: Das Axiom von Pasch
- Gegeben sei ein Dreieck
 . Ferner sei
. Ferner sei  eine Gerade, die durch keinen der drei Eckpunkte
eine Gerade, die durch keinen der drei Eckpunkte  geht. Wenn
geht. Wenn  eine der drei Seiten des Dreiecks
eine der drei Seiten des Dreiecks  schneidet, dann schneidet
schneidet, dann schneidet  genau eine weitere Seite des Dreiecks
genau eine weitere Seite des Dreiecks  .
.
Axiom IV.1 (Winkelmaßaxiom)
- Zu jedem Winkel
 gibt es genau eine reelle Zahl
gibt es genau eine reelle Zahl 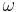 zwischen 0 und 180.
zwischen 0 und 180.
- Zu jedem Winkel
Axiom IV.2: (Winkelkonstruktionsaxiom)
- Es sei
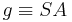 eine Gerade in der Ebene
eine Gerade in der Ebene  . Zu jeder reellen Zahl
. Zu jeder reellen Zahl 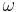 mit
mit 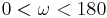 gibt es in jeder der beiden durch
gibt es in jeder der beiden durch  bestimmten Halbebenen der Ebene
bestimmten Halbebenen der Ebene  genau einen Strahl
genau einen Strahl 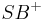 mit
mit 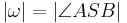
- Es sei
Axiom IV.3: (Winkeladditionsaxiom)
- Wenn der Punkt
 zum Inneren des Winkels
zum Inneren des Winkels  gehört , dann gilt
gehört , dann gilt 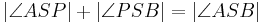 .
.
- Wenn der Punkt
Axiom IV.4: (Supplementaxiom)
- Nebenwinkel sind supplementär.
Axiom V: (Kongruenzaxiom SWS)
- Wenn für zwei Dreiecke
 und
und  die folgenden 3 Kongruenzen
die folgenden 3 Kongruenzen
- Wenn für zwei Dreiecke
- gelten,
- dann sind die beiden Dreiecke
 und
und  kongruent zueinander.
kongruent zueinander.
Definitionen
Definition I/2: (kollinear)
- Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
- Schreibweise: koll(A, B, C, ...) Sollten die Punkte A, B, C einer Menge nicht kollinear sein, so schreibt man:nkoll(A, B, C)
Definition I/3: (Inzidenz Punkt Ebene)
- Ein Punkt P inzidiert mit einer Ebene E, wenn P ein Element der Ebene E ist.
Definition I/4: (Inzidenz Gerade Ebene)
- Eine Gerade g gehört zu einer Ebene E, wenn jeder Punkt von g zu E gehört.
Definition I/5: (Raum)
- Die Menge aller Punkte P wird Raum genannt.
Definition I/6: (komplanar)
- Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(A, B, C, D, ...) (analog nkomp(..) für nicht komplanar)
Definition I/7: (komplanar für Geraden)
- Zwei Geraden g und h sind komplanar, wenn es eine Ebene gibt, in der beide Geraden vollständig liegen.
- Schreibweise: komp(g, h)
Definition I/8: (Geradenparallelität)
- Zwei Geraden g und h sind parallel, wenn sie identisch oder komplanar und schnittpunktfrei sind.
- In Zeichen: g||h.
Definition I/9: (windschief )
- Zwei Geraden g und h sind windschief, wenn sie schnittpunktfrei und nicht parallel sind.
Definition I/10: (parallel für Ebenen)
- Zwei Ebene E1 und E2 sind parallel, wenn sie keinen Punkt gemeinsam haben.
Definition II.1: (Abstand)
- Der Abstand zweier Punkte
 und
und  ist die Zahl, die nach dem Abstandsaxiom den Punkten
ist die Zahl, die nach dem Abstandsaxiom den Punkten  und
und  zugeordnet werden kann.
zugeordnet werden kann.
Schreibweise: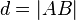 .
.
Definition II.2: (Zwischenrelation)
- Ein Punkt
 liegt zwischen zwei Punkten
liegt zwischen zwei Punkten  und
und  , wenn
, wenn  gilt und der Punkt
gilt und der Punkt  sowohl von
sowohl von  als auch von
als auch von  verschieden ist.
verschieden ist.
- Schreibweise:

Definition II.3: (Strecke, Endpunkte einer Strecke)
- Es seien
 und
und  zwei verschiedene Punkte. Die Punktmenge, die
zwei verschiedene Punkte. Die Punktmenge, die  und
und  sowie alle Punkte, die zwischen
sowie alle Punkte, die zwischen  und
und  liegen, enthält, heißt Strecke
liegen, enthält, heißt Strecke  . Stimmt das? --Sternchen 13:07, 5. Jun. 2010 (UTC)
. Stimmt das? --Sternchen 13:07, 5. Jun. 2010 (UTC)
- Es seien
Definition II.4: (Länge einer Strecke)
- Es seien
 und
und  zwei verschiedene Punkte. Der Abstand
zwei verschiedene Punkte. Der Abstand 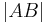 heißt Länge der Strecke
heißt Länge der Strecke  . OK? --Sternchen 13:09, 5. Jun. 2010 (UTC)
. OK? --Sternchen 13:09, 5. Jun. 2010 (UTC)
- Es seien
Definition II.5: (Halbgerade, bzw. Strahl)
Eine informelle Definition:
Definition: Halbgerade 
- Gegeben seien zwei verschiedene Punkte
 und
und  . Unter dem Strahl bzw. der Halbgeraden
. Unter dem Strahl bzw. der Halbgeraden 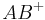 versteht man die Strecke
versteht man die Strecke  vereinigt mit der Menge aller der Punkte, die man erhält, wenn man
vereinigt mit der Menge aller der Punkte, die man erhält, wenn man  über
über  hinaus verlängert.
hinaus verlängert.
- Gegeben seien zwei verschiedene Punkte
Formulieren Sie eine mathematisch korrekte Definition des Begriffs Halbgerade 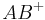 .
.
- Definition: Halbgerade

- Definition: Halbgerade
diese Lösung ist richtig!--Schnirch 12:48, 16. Jun. 2010 (UTC)
Gegeben seien zwei nicht identische Punkte  und
und  . Unter
. Unter 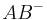 wollen wir die Menge aller Punkte
wollen wir die Menge aller Punkte  verstehen, die man erhält, wenn man
verstehen, die man erhält, wenn man  über
über  hinaus verlängert. Geben Sie eine mathematisch korrekte Definition für die Menge dieser Punkte
hinaus verlängert. Geben Sie eine mathematisch korrekte Definition für die Menge dieser Punkte  an.
an.
Lösung: Ergänzen Sie einfach die folgende Mengenschreibweise:
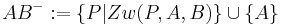
diese Lösung ist richtig! --Schnirch 12:49, 16. Jun. 2010 (UTC)
Definition III.1: (Mittelpunkt einer Strecke)
- Wenn ein Punkt
 der Strecke
der Strecke  zu den Endpunkten
zu den Endpunkten  und
und  jeweils den selben Abstand hat, dann ist er der Mittelpunkt der Strecke
jeweils den selben Abstand hat, dann ist er der Mittelpunkt der Strecke  .
.
Definition IV.1: (offene Halbebene)
- Es sei
 eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Punktmengen:
versteht man die folgenden Punktmengen:
- Es sei
muss es nicht heißen: 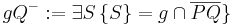 \ g
\ g
da es sich um eine offene Halbebene handelt, darf g doch nicht enthalten sein, oder? --Frühling 15:10, 28. Jun. 2010 (UTC)
Definition IV.2: (Halbebene)
- Es sei
 eine Gerade der Ebene
eine Gerade der Ebene  .
.  und
und 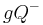 seien die beiden offenen Halbebenen von
seien die beiden offenen Halbebenen von  bezüglich
bezüglich  . Unter den (geschlossenen) Halbebenen von
. Unter den (geschlossenen) Halbebenen von  bezüglich
bezüglich  versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von
versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von  bezüglich der Geraden
bezüglich der Geraden  mit jeweils dieser Geraden
mit jeweils dieser Geraden  entstehen.
entstehen.
- Es sei
- Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene:
 , (geschlossene) Halbebene:
, (geschlossene) Halbebene:  . Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass
. Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass  bzw.
bzw. 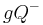 immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
- --*m.g.* 21:50, 23. Jun. 2010 (UTC)
- Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene:
Dies habe ich aus dem Skript kopiert. --Rakorium 11:43, 7. Jul. 2010 (UTC)
Definition IV.3: (konvexe Punktmenge)
- Eine Menge
 von Punkten heißt konvex, wenn mit je zwei Punkten
von Punkten heißt konvex, wenn mit je zwei Punkten  und
und  dieser Menge die gesamte Strecke
dieser Menge die gesamte Strecke  zu
zu  gehört.
gehört.
- Eine Menge
Definition V.1: (Winkel)
- Ein Winkel heißt die Vereinigungsmenge zweier Strahlen p und q, die einen gemeinsamen Anfangspunkt S haben.
oder
- Ein Winkel ist ein Paar Halbgeraden p, q mit gemeinsamen Anfangspunkt S.
Definition V.2: (Inneres eines Winkels)
- Das Innere eines Winkels
 ist der Schnitt ...der beiden Halbebenen
ist der Schnitt ...der beiden Halbebenen 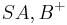 und
und 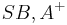
- Das Innere eines Winkels
Definition V.3: (Scheitelwinkel)
- Die Winkel
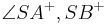 und
und 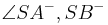 sind Scheitelwinkel.
sind Scheitelwinkel.
- Die Winkel
Definition V.4: (Nebenwinkel)
- Die Winkel
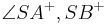 und
und 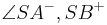 sind Nebenwinkel.
sind Nebenwinkel.
- Die Winkel
Definition V.5: (Größe eines Winkels)
- Die Zahl
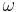 , die entsprechend des Winkelmaßaxioms einem jeden Winkel
, die entsprechend des Winkelmaßaxioms einem jeden Winkel  eindeutig zugeordnet werden kann, wird die Größe oder das Maß von
eindeutig zugeordnet werden kann, wird die Größe oder das Maß von  genannt.
genannt.
In Zeichen: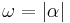 .
.
- Die Zahl
Definition V.6 : (Rechter Winkel)
- Wenn ein Winkel die selbe Größe wie einer seiner Nebenwinkel hat, so ist er ein rechter Winkel.
Definition V.7 : (Supplementärwinkel)
- Zwei Winkel heißen genau dann supplementär, wenn die Summe ihrer Größen 180 beträgt.
Definition V.8 : (Relation senkrecht auf der Menge der Geraden)
- Es seien
 und
und  zwei Geraden. Wenn sich
zwei Geraden. Wenn sich  und
und  schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden
schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden  und
und  senkrecht aufeinader.
senkrecht aufeinader.
- Es seien
- In Zeichen:
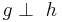 (in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
(in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
- In Zeichen:
Definition V.9 : (noch mehr Senkrecht)
- Eine Gerade
 und eine Strecke
und eine Strecke  stehen senkrecht aufeinander, wenn die
stehen senkrecht aufeinander, wenn die  und die Gerade
und die Gerade  senkrecht aufeinander stehen.
senkrecht aufeinander stehen.
- Eine Gerade
Ergänzen Sie:
- Eine Strecke
 und eine Strecke
und eine Strecke 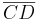 stehen senkrecht aufeinander, wenn ... die Gerade AB und die Gerade CD senkrecht aufeinander stehen??? --Maude001 11:45, 27. Jun. 2010 (UTC)
stehen senkrecht aufeinander, wenn ... die Gerade AB und die Gerade CD senkrecht aufeinander stehen??? --Maude001 11:45, 27. Jun. 2010 (UTC)
- Eine Strecke
- Eine Gerade
 und eine Ebene
und eine Ebene  stehen senkrecht aufeinander, wenn es in
stehen senkrecht aufeinander, wenn es in  ... zwei Geraden gibt, die nicht parallel oder identisch sind und vollständig in
... zwei Geraden gibt, die nicht parallel oder identisch sind und vollständig in  liegen und auf die
liegen und auf die  senkrecht steht. --Löwenzahn 15:18, 2. Jul. 2010 (UTC)
senkrecht steht. --Löwenzahn 15:18, 2. Jul. 2010 (UTC)
- Eine Gerade
Sätze
Satz I.1
- Es seien g und h zwei Geraden. Wenn g und h nicht identisch sind, haben sie höchstens einen Punkt gemeinsam.
Satz I.2: (Kontraposition von Satz I.1)
- Es seien g und h zwei Geraden.
- Wenn g und h mehr als einen Punkt gemeinsam haben, so sind g und h identisch.
Satz I.3: (Existenz von drei Geraden)
- Es existieren mindestens drei paarweise verschiedene Geraden.
Satz I.5:
- Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
Satz I.6:
- Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
Satz I.7:
- Jede Ebene enthält (wenigstens) drei Punkte.
Satz II.1
- Aus
 folgt
folgt 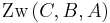 .
.
Satz II.2:
- Aus
 folgt
folgt  .
.
Satz II.3
- Es sei
 mit
mit  sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt oder
oder 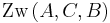 oder
oder 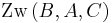 .
.
Satz II.4
- Es sei
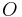 ein Punkt einer Geraden
ein Punkt einer Geraden  .
.
Die Teilmengen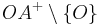 ,
, 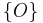 und
und 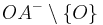 bilden eine Klasseneinteilung der Geraden
bilden eine Klasseneinteilung der Geraden  .
.
Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke)
- Jede Strecke hat genau einen Mittelpunkt.
Satz IV.1: (Repräsentantenunabhängigkeit)
- Wenn
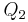 ein Punkt der Halbebene
ein Punkt der Halbebene 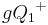 ist, dann gilt
ist, dann gilt 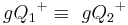 und
und  .
.
Satz IV.2
- Halbebenen sind konvexe Punktmengen
Satz IV.3
- Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Satz V.1
- Das Innere eines Winkels ist konvex.
Satz V.2
- Wenn der Punkt
 im Inneren des Winkels
im Inneren des Winkels  und nicht auf einem der Schenkel des Winkels
und nicht auf einem der Schenkel des Winkels  liegt, dann ist die Größe der beiden Teilwinkel
liegt, dann ist die Größe der beiden Teilwinkel 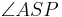 und
und 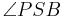 jeweils kleiner als die Größe des Winkels
jeweils kleiner als die Größe des Winkels  .
.
Satz V.3 : (Existenz von rechten Winkeln)
- Es gibt rechte Winkel.
Satz V.4 :
- Jeder rechte Winkel hat das Maß 90.
Satz V.5 : ( Existenz und Eindeutigkeit der Senkrechten in einem Punkt)
- Gegeben seien ein Punkt P auf einer Geraden g in einer Ebene E. Es gibt in E genau eine Gerade, die durch P geht und senkrecht auf g steht.
oder
- Es sei
 eine Gerade der Ebene
eine Gerade der Ebene  . Ferner sei
. Ferner sei  ein Punkt auf
ein Punkt auf  . In der Ebene
. In der Ebene  gibt es genau eine Gerade
gibt es genau eine Gerade 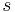 , die durch
, die durch  geht und senkrecht auf
geht und senkrecht auf  steht.
steht.
Satz VI.1: (Existenz und Eindeutigkeit der Mittelsenkrechten)
- Jede Strecke hat in jeder Ebene, zu der die Strecke vollständig gehört, genau eine Mittelsenkrechte.
Satz VI.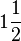
- Es sei
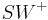 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels  . Dann gilt
. Dann gilt 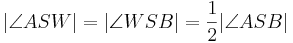 .
.
- Es sei
Satz VI.2 (Existenz und Eindeutigkeit der Winkelhalbierenden)
- Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Satz VII.1:
- Die Relation kongruent ist auf der Menge aller Strecken eine Äquivalenzrelation.
Satz VII.2:
- Die Relation kongruent ist auf der Menge aller Winkel eine Äquivalenzrelation.
Satz VII.3:
- Die Relation kongruent ist auf der Menge aller Dreiecke eine Äquivalenzrelation.
Satz VII.4: (Kongruenzsatz WSW)
- Wenn für zwei Dreiecke
 und
und  die folgenden 3 Kongruenzen
die folgenden 3 Kongruenzen
- Wenn für zwei Dreiecke
- gelten,
- dann sind die beiden Dreiecke
 und
und  kongruent zueinander.
kongruent zueinander.
Satz VII.5: Basiswinkelsatz
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Lemma 1
- Die Winkelhalbierende
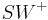 eines Winkels
eines Winkels  schneidet die Strecke
schneidet die Strecke  in genau einem Punkt
in genau einem Punkt  .
.
- Die Winkelhalbierende
Satz VII.6: (Mittelsenkrechtenkriterium)
- Eine Menge
 von Punkten ist genau dann die Mittelsenkrechte einer Strecke
von Punkten ist genau dann die Mittelsenkrechte einer Strecke  , wenn für jeden Punkt
, wenn für jeden Punkt 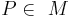 gilt:
gilt: 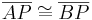 .
.
- Eine Menge
Satz VII.6 a: (hinreichende Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von  gehört.)
gehört.)
- Wenn ein Punkt
 zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von  .
.
- Wenn ein Punkt
Satz VII.6 b (notwendige Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von  gehört)
gehört)
- Wenn ein Punkt
 zur Mittelsenkrechten der Strecke
zur Mittelsenkrechten der Strecke  gehört, dann hat er zu den Punkten
gehört, dann hat er zu den Punkten  und
und  ein und denselben Abstand.
ein und denselben Abstand.
- Wenn ein Punkt