Lösung von Aufgabe 11.7
Beweisen Sie Satz VII.6a:
Wenn ein Punkt  zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von  .
.
Versuch 1:
VSS: Punkt P,  ,
,  , Mittelsenkrechte m
, Mittelsenkrechte m
Beh: 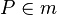
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 
|
(VSS) |
| (II) | es existiert ein Punkt 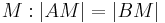
|
Existenz und Eindeutigkeit Mittelpunkt (I) |
| (III) | 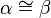
|
Basiswinkelsatz |
| (IV) | 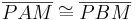
|
(I), (II), (III), (SWS) |
| (V) | 
|
(Def Dreieckskongruenz) (IV) |
| (VI) | 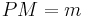
|
(Axiom I.1), (II), (V) |
--> 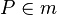 , die Behauptung ist wahr.
, die Behauptung ist wahr.
qed --Löwenzahn 13:52, 4. Jul. 2010 (UTC)
Welches Winkel sind 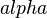 und
und 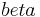 und welche Bedingungen müssen erfüllt sein, dass der Basiswinkelsatz überhaupt angewandt werden kann? Schritt 3 muss nochmal überprüft werden! Ist ein kongruenter Winkel überhaupt nötig? Warum nicht der Kongruentssatz SSS?
und welche Bedingungen müssen erfüllt sein, dass der Basiswinkelsatz überhaupt angewandt werden kann? Schritt 3 muss nochmal überprüft werden! Ist ein kongruenter Winkel überhaupt nötig? Warum nicht der Kongruentssatz SSS?
--Tja??? 13:06, 10. Jul. 2010 (UTC)
Die Winkel 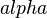 und
und 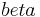 entsprechen den Winkel
entsprechen den Winkel 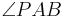 und
und 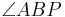 . Die Kongruenz dieser Winkel ist nötig, um den Satz über SWS zu beweisen. Wenn du den Satz über SSS beweist, dann brauchst du die Winkel logischer Weise nicht. --Löwenzahn 15:27, 10. Jul. 2010 (UTC)
. Die Kongruenz dieser Winkel ist nötig, um den Satz über SWS zu beweisen. Wenn du den Satz über SSS beweist, dann brauchst du die Winkel logischer Weise nicht. --Löwenzahn 15:27, 10. Jul. 2010 (UTC)
Versuch 2:
VSS:
- Punkt P, Strecke
 , es gilt
, es gilt 
- Mittelsenkrechte m; für die gilt laut Definition: senkrecht zu
 und geht durch
und geht durch 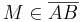 und es gilt:
und es gilt: 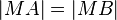
Behauptung: 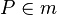
Annahme (indirekter Beweis): 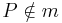
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Das Dreieck 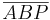 ist gleichschenklig ist gleichschenklig
|
Definition gleichschenkliges Dreieck, da laut VSS 
|
| (II) | 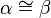
|
Basiswinkelsatz |
| (III) | Es existiert eine Winkelhalbierende w des winkels 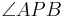
|
Satz VI.2 (Existenz und Eindeutigkeit der Winkelhalbierenden): Zu jedem Winkel gibt es genau eine Winkelhalbierende. |
| (IV) | Die Winkelhalbierende w und die Strecke  schneiden sich in schneiden sich in 
|
... (Skizze? Reicht das als Begründung?)
Nein, Satz: Ist SP+ ein Strahl im Inneren des Winkels <ASB, so schneidet er die Strecke |
| (VI) | SWS: 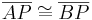 (VSS) (VSS) 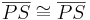 (trivial) (trivial) 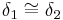 (III) (III)
| |
| (VII) | 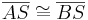
|
Dreieckskongruenz: (VI) |
| (VIII) | 
|
(VII), Existenz und Eindeutigkeit eines Mittelpunktes, da laut (VSS) gilt: 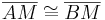
|
| (IX) | 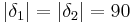
|
Dreieckskongruenz: (VI), kongruente Nebenwinkel sind rechte Winkel |
| (X) | 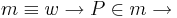 Widerspruch zu Annahme! Widerspruch zu Annahme!
|
(VIII), (IX), (III), (VSS) |
Einige Schritte sind zum besseren Verständnis in kleinste Einheiten aufgeteilt, deswegen sind es letztlich 10 Beweisschritte. Die Grundidee ist simpel: mit der Winkelhalbierenden erzeugt man zwei kongruente Dreiecke. Analog zur Lösung 1, wo der Knackpunkt der Mittelpunkt der Basis (gleichschenkliges Dreieck) ist, läuft der Beweis ab der Winkelhalbierenden "automatisch" durch.
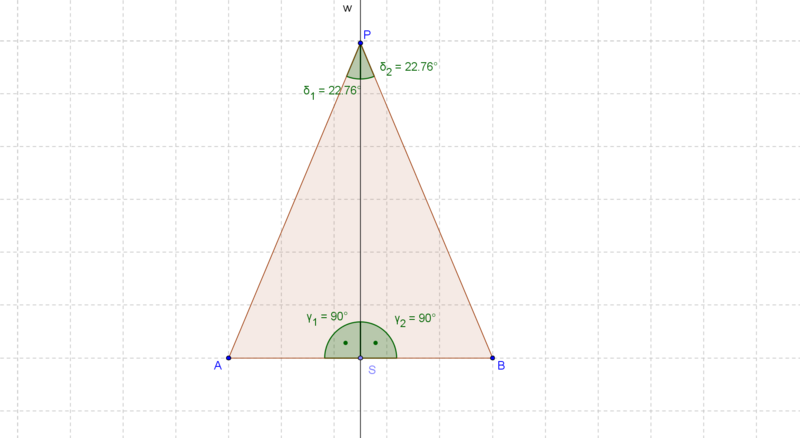
--Heinzvaneugen 12:19, 10. Jul. 2010 (UTC)

