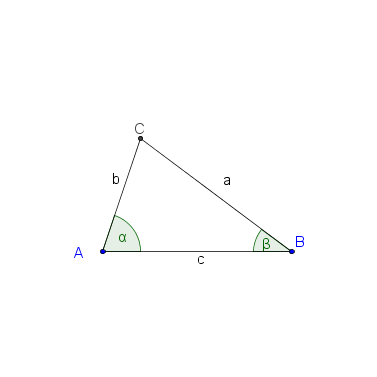
Beziehungen zwischen den Seitenlängen und den Innenwinkelgrößen eines Dreiecks
Inhaltsverzeichnis |
Satz IX.2: (Der größeren Seite liegt der größere Winkel gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
- Es sei
Beweis von Satz IX.2
Es sei  ein Dreieck.
ein Dreieck.
Voraussetzung:
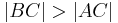 bzw.
bzw. 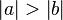
Nach dem Dreieck müsste es doch heißen:
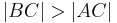 --Heinzvaneugen 18:12, 20. Jul. 2010 (UTC)
--Heinzvaneugen 18:12, 20. Jul. 2010 (UTC)
Ist das denn wichtig? Ich denke es ist nur eine Skizze, die die Bezeichnungen klärt, nicht aber Größenverhältnisse abbilden muss. Diese wiederum klärt die Voraussetzung und die Behauptung. --Maude001 19:59, 21. Jul. 2010 (UTC)
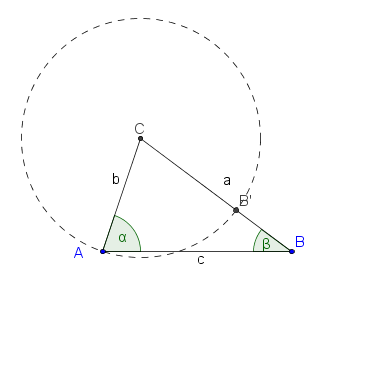
Auf  gibt es jetzt genau einen Punkt
gibt es jetzt genau einen Punkt 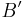 mit
mit 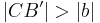 .
.
Denke ich falsch, oder soll es heißen 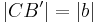 ??? --Maude001 11:25, 17. Jul. 2010 (UTC)
??? --Maude001 11:25, 17. Jul. 2010 (UTC)
Ich würde auch sagen, dass da ein "=" hinmuss.--Löwenzahn 11:43, 17. Jul. 2010 (UTC)
Begründung der Konstruktion von 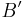 :
:
...
Nach Voraussetzung 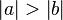 und dem Axiom vom Lineal. --Maude001 11:29, 17. Jul. 2010 (UTC)
und dem Axiom vom Lineal. --Maude001 11:29, 17. Jul. 2010 (UTC)
Wie geht es weiter?
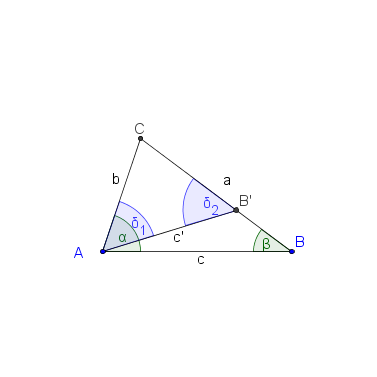
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (i) | 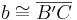
|
nach Konstruktion---mogli- 15:45, 17. Jul. 2010 (UTC) |
| (ii) | 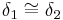
|
nach Basiswinkelsatz---mogli- 15:45, 17. Jul. 2010 (UTC) |
| (iii) | 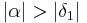
|
da 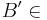 (der offenen Strecke) (der offenen Strecke)  , liegt , liegt 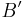 im Inneren von im Inneren von  , nach "Geschichten aus dem Inneren" --Löwenzahn 10:05, 18. Jul. 2010 (UTC) , nach "Geschichten aus dem Inneren" --Löwenzahn 10:05, 18. Jul. 2010 (UTC)
|
| (iv) | 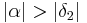
|
(ii), (iii) --Löwenzahn 10:05, 18. Jul. 2010 (UTC) |
| (v) | 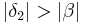
|
schwacher Außenwinkelsatz --Löwenzahn 10:05, 18. Jul. 2010 (UTC) |
| (vi) | 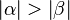
|
(iv), (v) --Löwenzahn 10:05, 18. Jul. 2010 (UTC) |
Satz IX.3: (Dem größeren Winkel liegt die größere Seite gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 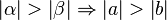
- Es sei
Beweis von Satz IX.3
Es sei  ein Dreieck.
ein Dreieck.
Voraussetzung:
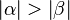
Behauptung:
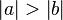
Annahme:
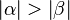
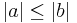
Es ergeben sich sofort zwei Widersprüche. Welche?
1.) Wenn a = b, dann ist 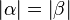
2.) Wenn a < b, dann ist 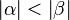 ---mogli- 15:44, 17. Jul. 2010 (UTC)
---mogli- 15:44, 17. Jul. 2010 (UTC)
korrekt
Sie müssen allerdings noch begründen, warum sich diese Widersprüche ergeben. Für die Führung eines indirekten Beweises isr es ferner wichtig, aufzuzeigen, wozu sich der Widerspruch ergibt. --*m.g.* 06:38, 19. Jul. 2010 (UTC)
Begründung:
Voraussetzung: 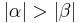
Annahme: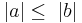
Aus "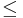 " lassen sich zwei Fälle ableiten:
" lassen sich zwei Fälle ableiten:
- )
 , dann gilt allerdings
, dann gilt allerdings 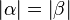 , da es sich um ein gleichschenkliges Dreieck handelt, bei dem bekanntlich die Basiswinkel kongruent sind --> Widerspruch zur VSS!
, da es sich um ein gleichschenkliges Dreieck handelt, bei dem bekanntlich die Basiswinkel kongruent sind --> Widerspruch zur VSS!
- )
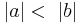 , das ist allerdings der Fall, wenn
, das ist allerdings der Fall, wenn 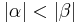 , siehe Beweis "Satz IX.2" --> Widerspruch zu VSS! (Oder muss an dieser Stelle der Beweis der Umkehrung geführt werden?)
, siehe Beweis "Satz IX.2" --> Widerspruch zu VSS! (Oder muss an dieser Stelle der Beweis der Umkehrung geführt werden?)
--Heinzvaneugen 18:25, 20. Jul. 2010 (UTC)