Der Zentriwinkel-Peripheriewinkelsatz

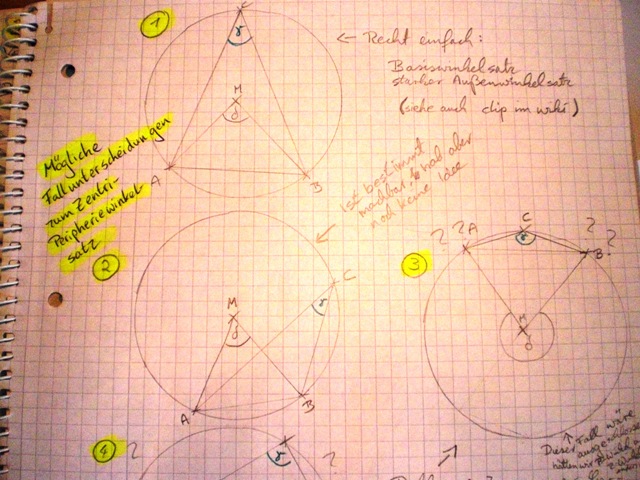
Idee des Beweises eines Spezialfalls

Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?

Der Zentri-Peripheriewinkelsatz

Definition (Zentriwinkel, Mittelpunktswinkel)

Ist M der Mittelpunkt des Kreises k, so bezeichnet man einen Winkel 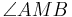$\angle AMB$ als den zughörigen Zentriwinkel (Mittelpunktswinkel).

Satz:(Der Zentri-Peripheriewinkelsatz)

(abgeändert) Jeder Peripheriewinkel ist halb so groß, wie sein zugehöriger Zentriwinkel.

Kommentar --*m.g.* 20:59, 23. Jul. 2010 (UTC): Vorsicht mit den Artikeln: Wie viele Zentriwinkel sind einem Peripheriewinkel zugehörig? In der Definition war es korrekt.

Beweis

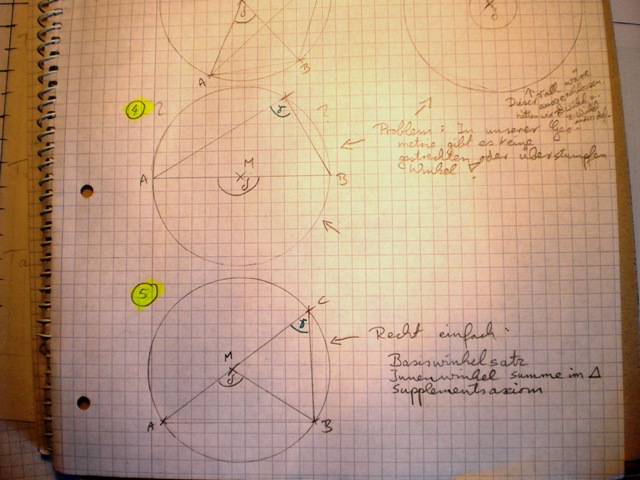
Ich hab mir Gedanken zu den Fallunterscheidungen gemacht, komme aber irgendwie nicht weiter. Ich stelle meine Notizen mal hier ein, kann mir jemand weiter helfen?

--Barbarossa 13:22, 25. Jul. 2010 (UTC)

Jaaaaaaaaa :-) Ich glaube, ich hatte gerade DIE Eingebung, zumindest bezüglich der Fallunterscheidungen ;-).
Und zwar: Laut dem Peripheriewinkelsatz sind alle Peripheriewinkel eines Kreises über einer Sehne gleich groß. Ich kann also sagen, dass ich den Scheitelpunkt des Peripheriewinkels so wähle, dass er auf der Mittelsenkrechten der Sehne liegt. Damit würden zumindest die Fälle 2 und 5 wegfallen.
Hm, naja, ob es allerdings viel hilft? Denn schließlich wären ja gerade Fall 3 und 4 die "unmöglichen Beweise"... Egal, Hauptsache Eingebung :-)
--Barbarossa 12:45, 26. Jul. 2010 (UTC)

Überlegung--Löwenzahn 16:02, 26. Jul. 2010 (UTC)

1. Könnte ich nicht Fall 1 so umändern, dass Fall 5 daraus wird: Wegen dem Satz "Peripheriewinkel über ein und derselben Sehne sind kongruent zueinander". Dann könnte man wie bei Fall 5 weiter argumentieren und man hätte auch schon Fall 2 drin.
2. Fall 3 und 4 sind nicht beweisbar, wegen unserem Winkelmaß zwischen 0 und 180.
3. zu Fall 2: könnte man nicht hier auch wieder eine Strecke 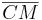$\overline {CM}$ konstruieren, wodurch wieder eine ähnliche Beweisführung wie bei Fall 1 eintritt?
   

Mal so ne blöde Frage zwischendurch: Haben wir schon bewiesen, dass der Radius immer gleich groß bleibt!?