Das Lot von einem Punkt auf eine Gerade (SoSe 11)
Inhaltsverzeichnis |
Der Begriff des Lotes
Definition IX.1: (Lot, Lotgerade, Lotfußpunkt)
- Es sei
 ein Punkt, der nicht zur Geraden
ein Punkt, der nicht zur Geraden  gehören möge. ...
gehören möge. ...
- Es sei
Definition:
Es sei  ein Punkt, der nicht zur Geraden
ein Punkt, der nicht zur Geraden  gehören möge, die Grade durch
gehören möge, die Grade durch  und
und  , die senkrecht zu g ist heißt Lotgerade. Der Schnittpunkt
, die senkrecht zu g ist heißt Lotgerade. Der Schnittpunkt  von
von  und
und  heißt Lotfußpunkt, die Strecke
heißt Lotfußpunkt, die Strecke  Lot.--Peterpummel 20:38, 2. Jul. 2011 (CEST)
Lot.--Peterpummel 20:38, 2. Jul. 2011 (CEST)
Der Schnittpunkt von 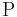 und
und 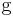 ... da
... da 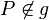 vorher in der Def. vorkommt, kann dies garnicht eintreten. --Tutor Andreas 10:33, 8. Jul. 2011 (CEST)
vorher in der Def. vorkommt, kann dies garnicht eintreten. --Tutor Andreas 10:33, 8. Jul. 2011 (CEST)
Es sei \ P ein Punkt, der nicht zur Geraden \ g gehören möge, die Gerade durch \ P und \ g, die senkrecht zu g ist heißt Lotgerade l. Der Schnittpunkt \ S von \ l und \ g heißt Lotfußpunkt, die Strecke \overline{SP} SP heißt Lot.--
Definition IX.2: (Abstand eines Punktes zu einer Geraden)
- Es sei
 ein Punkt außerhalb von
ein Punkt außerhalb von  . Der Abstand von
. Der Abstand von  zu
zu  ist ...
ist ...
- Es sei
Defintion:
Es sei  ein Punkt außerhalb von
ein Punkt außerhalb von  . Der Abstand von
. Der Abstand von  zu
zu  ist die Länge des Lots von
ist die Länge des Lots von  auf
auf 
--Peterpummel 20:40, 2. Jul. 2011 (CEST)
Es sei  ein Punkt außerhalb von
ein Punkt außerhalb von  . Der Abstand von
. Der Abstand von  zu
zu  ist eine nicht negative reelle Zahl d. --Teufelchen 18:40, 3. Jul. 2011 (CEST)
ist eine nicht negative reelle Zahl d. --Teufelchen 18:40, 3. Jul. 2011 (CEST)
Als Abstand eines Punktes P von einer Geraden g wird der Abstand |PQ| bezeichnet, wobei Q der Fußpunkt des Lotes von P auf g ist.--mm_l 11:51, 13. Jul. 2011 (CEST)
Existenz und Eindeutigkeit des Lotes
Satz IX.1: (Existenz und Eindeutigkeit des Lotes)
- Zu jedem Punkt
 außerhalb einer Geraden
außerhalb einer Geraden  gibt es genau ein Lot von
gibt es genau ein Lot von  auf
auf  .
.
- Zu jedem Punkt
Beweis der Existenz und Eindeutigkeit des Lotes:
Übungsaufgabe
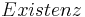
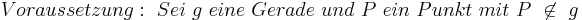
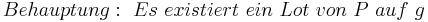
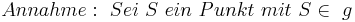

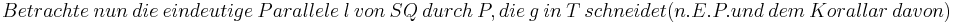
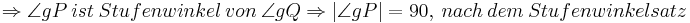
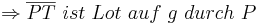
Die Eindeutigkeit der Parallele hatten wir schon in einer anderen Übung gezeigt, aus ihr folgt die Eindeutigkeit des Lots.--Peterpummel 13:30, 7. Jul. 2011 (CEST)
Ich glaube nicht, dass in einer Übung die Eindeutigkeit einer Parallelen gezeigt bzw. bewiesen wurde... vllt. wurde die Existens einer Parallelen gezeigt, aber wenn die Eindeutigkeit bewiesen worden wäre, dann widerspräche das dem Parallelenaxiom.--Tutor Andreas 10:38, 8. Jul. 2011 (CEST)
Anmerkung:
Das stimmt, aber aus der Existenz + dem EP => die Eindeutigkeit. In der Übung wurde nur das EP gefordert. Aus dem Stufenwinkelsatz folgt dann die Existenz.--Peterpummel 19:47, 9. Jul. 2011 (CEST)
Wenn du das EP oder den Stufenwinkelsatz verwendest, befindest du dich aber in der Euklidischen Geometrie und nicht mehr in der absoluten Geometrie. Es ist auch möglich, die Existenz des Lotes mit einer Hilfskonstruktion zu beweisen, indem
1) G ein Punkt auf g sei, in dem eine konstruierte Gerade durch P g schneidet
2) man den entstandenen Winkel misst (Winkelmaßaxiom)
3) man einen entsprechenden Winkel in der anderen Halbebene konstruiert (Winkelkonstruktionsaxiom)
4) man auf dem neu entstandenen Strahl einen Punkt P' abträgt, für den gilt 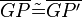 (Axiom vom Lineal)
(Axiom vom Lineal)
5) es entsteht ein Schnittpunkt L der Geraden g mit der Strecke 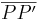
6) nach SWS (wir wissen, dass 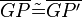 ,
, 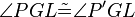 und
und 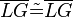 ) sind nun auch die Dreiecke kongruent und daher gilt auch
) sind nun auch die Dreiecke kongruent und daher gilt auch 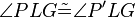
7) Da diese Winkel nun kongruente Nebenwinkel sind, sind es rechte Winkel. Daher wissen wir, dass 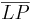 das Lot von P auf g ist.
das Lot von P auf g ist.
Hoffe mit der Darstellung ist die Idee verständlich. Die Eindeutigkeit ist recht schnell durch Widerspruch bewiesen. Geht man von einem zweiten Lot aus, kann man über den schwachen Außenwinkelsatz zeigen, dass nicht beide Winkel rechte Winkel sein können.--Matthias 15:18, 16. Jul. 2011 (CEST)

