12)
Wir gehen von folgender Definition aus:
Eine Winkelhalbierende eines Winkels  ist ein Strahl l, der im Inneren des Winkels
ist ein Strahl l, der im Inneren des Winkels  liegt, den Scheitel des Winkels
liegt, den Scheitel des Winkels  als Anfangspunkt besitzt und diesen Winkel in zwei gleich große Winkel
als Anfangspunkt besitzt und diesen Winkel in zwei gleich große Winkel 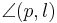 und
und 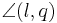 unterteilt.
unterteilt.
Außerdem sei folgende genetische Definition gegeben:
- Gegeben sei ein Winkel
 .
.
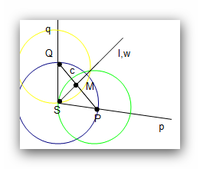
- Man konstruiere auf den beiden Schenkeln des Winkels
 zwei Punkte P und Q, die vom Scheitel S des Winkels
zwei Punkte P und Q, die vom Scheitel S des Winkels  gleich weit entfernt sind.
gleich weit entfernt sind.
- Man konstruiere die Strecke
 .
.
- Man konstruiere den Mittelpunkt M der Strecke
 .
.
- Man konstruiere den Strahl w mit dem Anfangspunkt S, der durch den Punkt M verläuft.
- Dieser Strahl w ist die Winkelhalbierende.
Beweisen Sie, dass durch diese Konstruktionsvorschrift tatsächlich die Winkelhalbierende entsprechend der angegebenen Definition entsteht.
- Wenn man die Konstruktionsvorschrift befolgt und eine Winkelhalbierende erhält, ist die Konstruktionsvorschrift dann bewiesen?
--Todah raba 18:06, 28. Okt. 2011 (CEST)
| Beweisschritt | Begründung |
(1)  = = 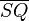 |
Voraussetzung |
(2) 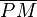 = = 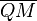 |
Konstruktionsvorschrift |
(3) 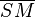 = = 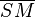 |
Konstruktionsvorschrift |
(4) 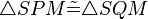 |
SSS,(1),(2),(3) |
(5) 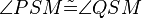 |
(4) |
--Mathenerds 10:40, 29. Okt. 2011 (CEST)
weiterer Lösungsversuch
- An dieser Stelle bitte ich den Autor einige Dinge näher zu erläutern, um eventuelle Missverständnisse zu vermeiden. --Tutor Andreas 14:40, 31. Okt. 2011 (CET)
Voraussetzungen:
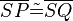
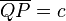 Was bedeutet c bzw c1 oder c2? Sind hier reelle Zahlen gemeint? --Tutor Andreas 14:40, 31. Okt. 2011 (CET)
c ist die Strecke von dem Punkt Q zu dem Punkt P--RicRic 14:27, 3. Nov. 2011 (CET)
Was bedeutet c bzw c1 oder c2? Sind hier reelle Zahlen gemeint? --Tutor Andreas 14:40, 31. Okt. 2011 (CET)
c ist die Strecke von dem Punkt Q zu dem Punkt P--RicRic 14:27, 3. Nov. 2011 (CET)
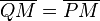
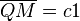 c1 ist die Stecke von dem Punkt Q zu dem Punkt M
c1 ist die Stecke von dem Punkt Q zu dem Punkt M
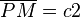 c2 ist die Stecke von dem Punkt P zu dem Punkt M--RicRic 14:27, 3. Nov. 2011 (CET)
c2 ist die Stecke von dem Punkt P zu dem Punkt M--RicRic 14:27, 3. Nov. 2011 (CET)
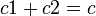
Behauptung:
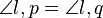
Beweis:
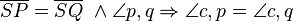 SWS Dreiecksatz berachtes Dreick: S,P,Q Wird hier wirklich der Kongruenzsatz SWS benutzt?
SWS Dreiecksatz berachtes Dreick: S,P,Q Wird hier wirklich der Kongruenzsatz SWS benutzt?
Was soll hier gemeint sein? --Tutor Andreas 14:40, 31. Okt. 2011 (CET)
- Ich betrachte hier das Dreieck S,P,Q und stelle fest, dass die Srecken S,Q und S,P der Voraussetzung nach gleich lang sind,
ebenfalls ist der Winkel q,p gegeben, daraus folgere ich, dass der Winkel c,p und der Winkel c,q konguent sein müssen. Da wenn bei einem Dreieck zwei aneinanderliegende Seiten und der dazwischenligende Winkel geben ist, die restlichen Winkel und die weitere Seite auch feststehen. Bei dem Sonderfall, dass die zwei Seiten, wie hier auch noch gleich lang sind müssen die Winkel auch konguent sein.
- Es wird mit deiner Bezeichnung noch nicht klar,welche Winkel du mit
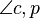 und
und 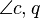 meinst. Denn wie ich das in der Zeichnung verstehe, beginnen der Strahl q und der Strahl p am Punkt S. Wo beginnt der Strahl c? Es wäre wohl klarer, wenn du die Strahlen durch Punkte bezeichnest.
meinst. Denn wie ich das in der Zeichnung verstehe, beginnen der Strahl q und der Strahl p am Punkt S. Wo beginnt der Strahl c? Es wäre wohl klarer, wenn du die Strahlen durch Punkte bezeichnest.
- Wenn dann die Bezeichnungen klar sind und du weißt, dass das Dreieck
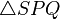 gleichschenklig ist, dann kannst du mit einem Satz (wohl auch aus der Schule bekannt) beweisen, dass die Winkel
gleichschenklig ist, dann kannst du mit einem Satz (wohl auch aus der Schule bekannt) beweisen, dass die Winkel 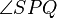 und
und 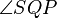 kongruent sind. Danach kann man dann kongruente Dreiecke vergleichen (welche sind das und mit welchem Satz kann man dies tun?) und somit zeigen, dass
kongruent sind. Danach kann man dann kongruente Dreiecke vergleichen (welche sind das und mit welchem Satz kann man dies tun?) und somit zeigen, dass 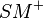 die Winkelhalbierende ist. --Tutor Andreas 09:49, 6. Nov. 2011 (CET)
die Winkelhalbierende ist. --Tutor Andreas 09:49, 6. Nov. 2011 (CET)
Vielen Dank erst mal. Okay dann verwernde ich hier den Basiswinkelsatz. Was dann beweist, dass diese Winkel konguent sind. --RicRic 09:51, 8. Nov. 2011 (CET)
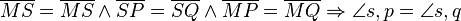 SSS Dreiecksatz betrachtete Dreicke S,M,P und S,Q,P.
SSS Dreiecksatz betrachtete Dreicke S,M,P und S,Q,P.
- Auch hier sind die Bezeichnungen nicht klar. Welcher Strahl ist der Strahl s? --Tutor Andreas 09:51, 6. Nov. 2011 (CET)
Korrektur: 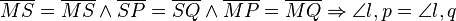 SSS Dreiecksatz betrachtete Dreicke S,M,P und S,Q,P.
SSS Dreiecksatz betrachtete Dreicke S,M,P und S,Q,P.
--RicRic 09:51, 8. Nov. 2011 (CET)
Somit muss die Halbgerade l die Winkelschneidende sein.--RicRic
Noch ein Versuch
| Beweisschritt | Begründung |
| (1) Dreieck SQM ist rechtwinklig | Satz des Tales |
| (2) Dreieck SMP ist rechtwinklig | Satz des Tales |
(3) 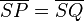 und und 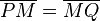 |
Konstruktionsvorschrift |
(4) sin(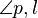 ) = ) = 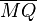 : :  |
Trigonometrie , (1) |
(5) sin(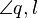 ) = ) = 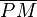 : :  |
Trigonometrie , (2) |
(6) sin(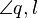 ) = ) = 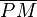 : :  = = 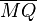 : :  |
(3) und (5) |
(7) sin(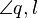 ) = sin( ) = sin(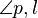 ) ) |
(6) und (4) |
(8) 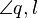 = = 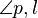 |
(7) |
--Flobold 14:21, 1. Nov. 2011 (CET)
Warum nutzt du bei (1)bzw.(2) den Satz des Thales?
Schritt (4) - (7) kannst du so machen (sofern Schritt (1) und (2)richtig begründet sind), allerdings braucht man wie oben zu sehen keine Trigometrie. --Tutorin Anne 10:12, 3. Nov. 2011 (CET)