12)
Aus Geometrie-Wiki
Version vom 8. November 2011, 14:50 Uhr von RicRic (Diskussion | Beiträge)
Im Seminar "Computer im Mathematikunterricht" hat eine Studentin eine Schatzkarte gefunden (siehe unten). Blöderweise ist auf der Insel die Feuerstelle bereits verschwunden.
- Können Sie den Schatz (Punkt M) trotzdem finden?
- Können Sie beweisen, dass das immer so funktioniert? (Es hat etwas mit den Eigenschaften von Parallelogrammen zu tun - siehe Hilfestelltung)
- Ich bin nicht ganz sicher, aber es fehlen hier doch einfach ein paar Angaben zur Aufgabe, oder?? --LouStick 13:30, 1. Nov. 2011 (CET)
- Ja, ich verstehe auch nicht, was man an dieser Stelle machen soll ^^wenn das vielleicht nochmal jemand erläutern könnte... --Miriam 17:18, 1. Nov. 2011 (CET)
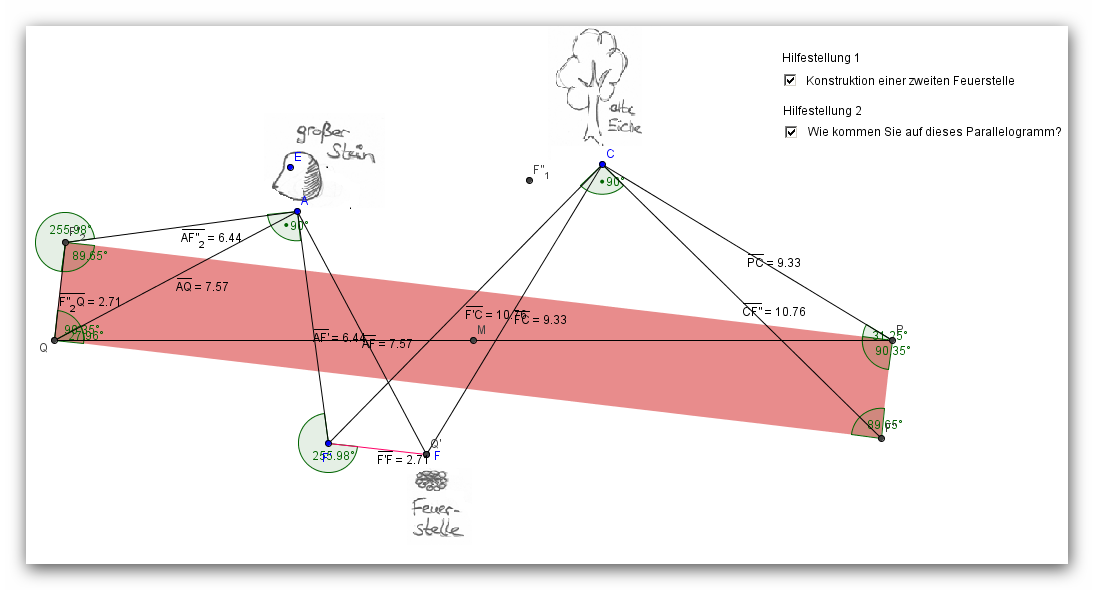
- Also ich nenne den Punkt am Stein A und den an der Eiche C. Es zeigt sich die Winkel an A und C jeweils 90° sind. Die Strecken A,Q und A,F sind konguent, die Strecken C,F und C,P ebenfalls. Wenn nun also der Punkt F für Feuerstelle nicht mehr auf den Insel vorhanden ist, setzt man zunächst einen willkürlichen Punkt F`.Diesen Punkt F` verbindet man mit dem A dem Stein und C der Eiche. Hier zeichnet man jeweils im gleichen Winkel 90° eine gleichlange (konguente) Strecke ein und erhält an den Endpunkten der Strecken somit die Punkte (einen davon habe ich F`` genannt) welche man mit den Punkten Q und P zu einem Parallelogramm verbindet. Nun misst man den Winkel (auf meiner Zeichnung den Außenwinkel, der Innenwinkel ist natürlich auch möglich) an F`` im Parallelogramm sowie die Strecke F``,Q und überträgt diese (Winkel und Strecke) auf F`, am Zielpunkt findet man F. Somit es es möglich die Position von F zu bestimmen obwohl F nicht mehr da ist und somit kann auch der Schatz noch gefunden werden.
 --RicRic
--RicRic
Okay, jetzt haben wie den Schatz gefunden, aber mit welcher speziellen Eigenschaft der Parallelogramme hat das jetzt zu tun? --RicRic 14:50, 8. Nov. 2011 (CET)

