12)
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 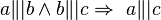 .
.
b) Welche Eigenschaft der Relation  auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
a) Vor.: a,b,c sind paarweise verschiedene Geraden Annahme: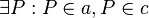
| 1 | Fehler beim Parsen(Unbekannte Funktion „\c“): \ a \|| b \c | Vor. |
| 2 | Fehler beim Parsen(Unbekannte Funktion „\c“): \ b \|| c \c | Vor. |
| 3 | 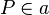 |
|
| 4 | 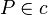 |
|
| 5 |  |
3,4 ; Widerspruch zur Vorraussetzung |
--Todah raba 20:07, 4. Nov. 2011 (CET)
b) Transitivität --Todah raba 20:07, 4. Nov. 2011 (CET)
Gebe dir in allem recht, würde nur sagen, dass es Aufgrund der Augabenstellung Sinn macht bei dem Beweis den Schritt 5 eher so zu formulieren:
| 5 | 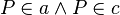 |
3,4 ; Widerspruch zum Parallelaxionom, Durch jeden Punkt kann nur eine Gerade gehen welche Parallel zu b ist. |
Bei der Annahme eventuell noch ergänzen, dass es sich beim dem Punkt P um den Schnittpunkt der beiden Geraden a und c handelt, von welchen wir ja annehmen, dass die nicht parallel sind und somit diesen Schnittpunkt haben müssen.--RicRic 18:13, 5. Nov. 2011 (CET)
@RicRic Meine Vorrausetzung ist doch, dass die Geraden a, b, c paarweise verschieden sind. Wenn ich in meiner Annahme davon ausgehe, dass P sowohl Element der Geraden a als auch der Geraden c ist, dann ist doch die einzige Möglichkeit, dass der Punkt P ein Schnittpunkt der Geraden a und c ist, oder? Muss ich es dann noch zusätzlich ergänzen? --Todah raba 18:23, 6. Nov. 2011 (CET)
- Die Annahme macht deutlich, dass P der Schnittpunkt von a und c ist. --Tutor Andreas 10:29, 10. Nov. 2011 (CET)
@Todah raba. Klar hast du Recht. Ich musste nur erst mal ne Weile darüber nachdenken bis ich es verstanden hatte. Deshalb finde ich es leichter zum Nachvollziehen. Stellt sich die Frage: Wird es falsch wenn mann zuviel angibt? Ähnlich wie bei Definitonen die so kurz wie möglich gehalten werden sollen. --RicRic 09:45, 8. Nov. 2011 (CET)
Würde es so auch gehen?
Vor: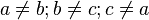
Fehler beim Parsen(Unbekannte Funktion „\c“): \ a \|| b \c und Fehler beim Parsen(Unbekannte Funktion „\c“): \ b \|| c \c
Beh: Fehler beim Parsen(Unbekannte Funktion „\c“): \ a \|| c \c
1. 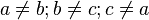 |
Vor |
2. Fehler beim Parsen(Unbekannte Funktion „\c“): \ a \|| b \c
und Fehler beim Parsen(Unbekannte Funktion „\c“): \ b \|| c \c |
Vor |
3. 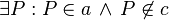 |
Vor( paarweise verschieden) |
| 4. Fehler beim Parsen(Unbekannte Funktion „\c“): \ a \|| c \c | 1,2,3, Parallelenaxiom |
was zu besweisen war.--Cmhock 20:24, 7. Nov. 2011 (CET)
Warum sollen die Geraden parallel sein, wenn ein Punkt existiert der Element der einen und nicht Element der anderen ist?--RicRic 09:45, 8. Nov. 2011 (CET)
Zur Veranschaulichung des Einwands:
--Tutor Andreas 10:39, 10. Nov. 2011 (CET)

