12)

Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
$\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace$

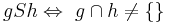
• reflexiv und symmetrisch --LouStick 18:33, 9. Nov. 2011 (CET)

• Die Relation lautet: g schneidet h. -> g kann sich nicht selbst schneiden.
  Ich würde sagen nur symmetrisch--Kulturschock 18:21, 14. Nov. 2011 (CET)
  • schneidet, ok - so könnte man sie nennen. Können sich zwei Geraden auch in zwei Punkten schneiden?

Ist die Relation nun reflexiv?
Und warum nicht transitiv?--Tutorin Anne 19:41, 16. Nov. 2011 (CET)

Ich denke ist nicht reflexiv, da wenn gRg steht, ist g geschnitten g die leere Menge und somit nicht in Relation.
Symetrisch auf jeden Fall, da g geschnitten h die gleiche Menge ist h geschnitten g.
Transistiv denke ich nicht, denn wenn g mit h einen Schnittpunkt gemeinsam hat und g mit i einen Schnittpunkt gemeinsam haben, muss nicht unbedingt h mit i einen Schnittpunkt haben.--RicRic 22:54, 16. Nov. 2011 (CET)

• Die Relation ist auf jeden Fall reflexiv, da eine Gerade g geschnitten mit sich selbst unendlich viele Schnittpunkte besitzt (da sie mit sich selbst identisch ist) :)--Miriam 11:32, 19. Nov. 2011 (CET)
• Es hilft vielleicht, wenn man sich die formale Schreibweise "übersetzt" oder vielleicht liegt das Problem bei etwas anderem... Eine Gerade g ist eine Punktmenge. Welche Elemente liegen denn im Schnitt, wenn man zwei Mengen schneidet (in unserem Fall 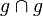$g \cap g$) bzw. was haben die Elemente, die im Schnitt zweier Mengen liegen, gemeinsam? --Tutor Andreas 11:04, 17. Nov. 2011 (CET)